Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 18
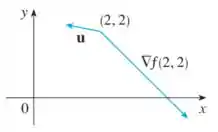
Use a figura para estimar .
Passo 1
Neste exercício, a partir da figura dada precisamos calcular a derivada direcional.
Começamos aproximando pontos iniciais e finais do vetor e, em seguida, calculando vetores e seu produto ponto.
O ponto inicial de cada vetor é . O ponto final de é aproximadamente e o ponto final de é aproximadamente .
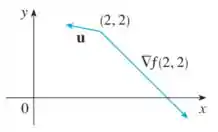
As aproximações são obtidas olhando para a figura e "adivinhando" a distância de , que é o único ponto dado.
Passo 2
Então vamos para os cálculos:
Temos então que o vetor unitário é dado por:
Agora finalmente calculamos o produto vetorial da nossa derivada direcional:
Resposta
Exercícios de Livros Relacionados
Determine a derivada direcional de f no ponto dado e na direção indicada por θ f x , y = y e - x , 0,4 , θ = 2 π 3
Calcule a derivada direcional de f x , y = 2 x 2 + y 2 No ponto (-1,1) e na direção 2i → + 3j → .
Uma função diferenciável f x , y tem, no ponto (1,1), derivada direcional igual a 3 na direção 3i → + 4j → e igual a -1 na direção 4i → - 3j → . Calcule: ∇ f → ( 1,1 ) ∂ f ∂ u → ( 1,1 ) onde u → é o v