Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 4
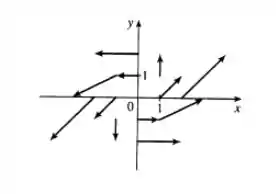
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .
Passo 1
Oi galera, tudo bem? Primeiro vamos começar vendo o tamanho desse vetor:
Aqui vamos notar que se , os vetores são verticais. Se forem na região apontam para cima. Se estiverem na região apontam para baixo.
Ok?
Passo 2
Vamos fazer uma tabela com alguns valores de e os respectivos vetores nesses pontos:
Num sistema cartesiano eles ficam assim ó:
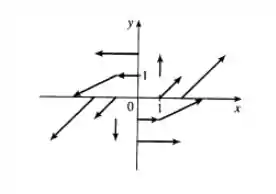
Resposta
Exercícios de Livros Relacionados
Calcular a integral do campo vetorial f → = ( - y , x ) ao longo dos seguintes caminhos fechados, no sentido anti-horário:Circunferência de centro na origem e raio 2;
Calcular a integral do campo vetorial f → = ( - y , x ) ao longo dos seguintes caminhos fechados, no sentido anti-horário:(b) elipse x 2 + 36 y 2 = 36
O campo de velocidade de um fluido em movimento é dado por v → = ( x , - y ) . Calcular a circulação do fluido ao redor da curva fechada C = C 1 ∪ C 2 ∪ C 3 , onde C 1 : Segmento de reta de A 0,0 e B
O campo de velocidade de um fluido em movimento é dado por v → = ( 2 x , 2 y , - z ) . Calcular a circulação do fluido ao redor da curva fechada C , sendo C dada por r → t = cos ti ^ + s e ntj ^ + 2
Calcular a integral do campo vetorial f → = ( - y , x ) ao longo dos seguintes caminhos fechados, no sentido anti-horário:(c) triângulo de vértices ( 1,1 ) , ( - 1,1 ) e ( 0 , - 1 )