Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.1 - Ex. 5
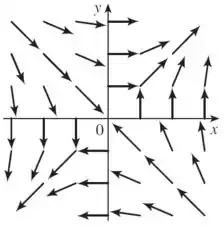
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .
Passo 1
Faaaaaala galerinha, beleza? Bora lá!
Temos um campo vetorial , e precisamos esboçar o seu diagrama como está na figura ou figura :
Beleza, mas como está na figura 5 ou 9? Vamos lembrar:
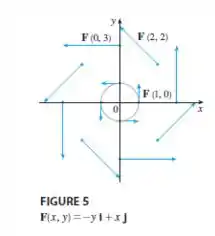
Veja a figura , o campo tem componentes vetoriais na direção e , assim o vetor pode ter várias direções e ele aumenta conforme se afasta da origem.
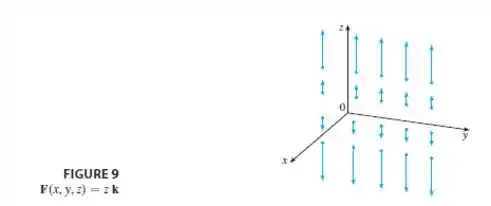
Na figura , temos um campo no espaço tridimensional. Repare que o campo tem apenas componente vetorial na direção , logo vamos ter apenas vetores na direção do eixo que aumentam conforme se afasta da origem.
Sabendo disso, nosso objetivo é avaliar o campo e fazer um esboço.
Quero que você repare uma coisa. Se pegarmos o seguinte vetor e dividirmos pela sua norma:
Sua norma é:
Dividindo o vetor pela sua norma , temos exatamente o vetor dado no enunciado:
E a gente sabe que todo vetor que é dividido pela sua norma, é um vetor unitário!!! Ou seja, ele tem tamanho fixo!! E compare o vetor abaixo com a Figura , você vai entender seu comportamento.
Assuma também alguns pontos aleatórios e veja o comportamento desse vetor.
Com esse bizu, vai ficar fácil!!! Vamos nessa!!
Passo 2
Temos o seguinte campo vetorial:
Já compreendemos do passo , que esse vetor é o seguinte vetor dividido pela sua norma:
Sua norma é:
Até aqui ok né!!! Sabe porque fizemos isso?
Porque fica mais fácil determinarmos como o campo vetorial se comporta, a partir desse vetor:
Passo 3
Vamos fazer uma tabela com alguns valores de e os respectivos vetores nesses pontos:
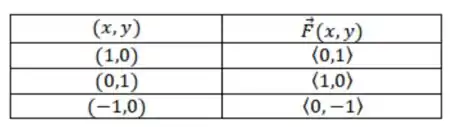
Quando falamos em relação aos quadrantes.
No primeiro quadrante o vetor sempre aponta no sentido positivo do eixo e .
No segundo quadrante, o vetor aponta no sentido positivo do eixo e no sentido negativo do eixo .
No terceiro quadrante, o vetor aponta no sentido negativo do eixo e .
Por fim, no quarto quadrante, o vetor aponta no sentido negativo do eixo e no sentido positivo do eixo .
Assim, sabendo o comportamento em cada quadrante, podemos esboçar o campo vetorial da seguinte forma no sistema cartesiano:
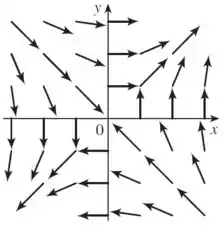
Resposta
