Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.4 - Ex. 12

Esboce a curva e calcule a área delimitada por ela.

r = 4 + 3 sen ⁡ θ

Passo 1

Olá, meu amigooo. Vamos resolver essa atividade aqui.

A gente tem a curva:

r = 4 + 3 sen ⁡ θ

E ela é dada em coordenadas polares. A gente precisa esboçar ela e precisamos calcular a área dessa curva.

O gráfico de   r = 4 + 3 sen ⁡ θ é, e a gente o gerou no GeoGebra:

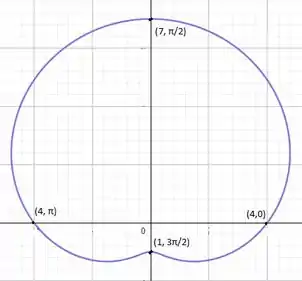
Lembrando que como estamos utilizando coordenadas polares os valores de r são positivos.

Vamos então integrar a fórmula para a área de uma região cuja fronteira é dada por uma equação polar.

A = ∫ 1 2 r 2 d θ

Passo 2

Os limites de integração podemos encontrar a partir do gráfico. A linha que forma a fronteira do gráfico começa a ‘varrer’ a figura em ( 4 ,   0 ) e da uma volta inteira, como você pode ver abaixo, ou seja, percorreu um ângulo θ = 2 π   r a d .

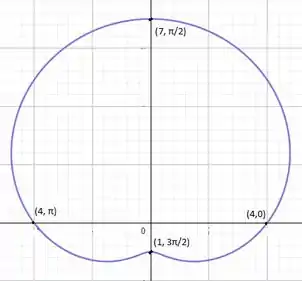
Aplicando os limites de integração   0 ≤ θ ≤ 2 π e substituindo r = 4 + 3   s e n   θ , obtemos:

A = ∫ 0 2 π 1 2 4 + 3   s e n   θ 2 d θ

A = 1 2 ∫ 0 2 π ( 16 + 24   s e n   θ + 9   s e n ² θ )   d θ  

Podemos usar a propriedade trigonométrica: s e n 2 θ = 1 2 1 - cos ⁡ 2 θ

A = 1 2 ∫ 0 2 π 16 + 24   s e n   θ + 9 2 1 - cos ⁡ 2 θ d θ

Realizando a distributiva e realizando a soma:

A = 1 2 ∫ 0 2 π 41 2 + 24   s e n   θ - 9 2 cos ⁡ 2 θ   d θ

Dividindo em diversas integrais:

A = 1 2 ∫ 0 2 π 41 2 d θ + 1 2 ∫ 0 2 π 24 sin ⁡ θ d θ - 1 2 ∫ 0 2 π 9 2 cos ⁡ 2 θ d θ

Realizando a integral de cada termo:

A = 1 2 ∙ 41 2 θ - 24   c o s   θ - 9 4 s e n   2 θ 0 2 π

Aplicando os limites de integração:

A = 1 2 ∙ 41 π - 24 - 0 - 0 - 24 - 0

A = 41 2 π

Resposta

A = 41 2 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os comprimentos das curvas nos exercícios 21-28.A curva r = cos 3 ⁡ θ / 3 ,0 ≤ θ ≤ π / 4 .
A área da região que está dentro da curva cardioide r = cos ⁡ θ + 1 e fora do circulo r = cos ⁡ θ não é 1 2 ∫ 0 2 π cos ⁡ θ + 1 2 - cos 2 ⁡ θ d θ = π Por que não? Qual é a área? Justifique suas respos
Encontre as áreas das regiões nos Exercícios 9-18Dentro da lemniscata r 2 = 6 cos ⁡ 2 θ e fora do círculo r = 3 .
Encontre os comprimentos das curvas nos exercícios 21-28.O segmento parabólico r = 2 / ( 1 - cos ⁡ θ ) ,π / 2 ≤ θ ≤ π .
Encontre as áreas das regiões nos Exercícios 9-18Dentro do círculo r = 4 cos ⁡ θ e à direita da reta vertical r = s e cθ .