Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 14
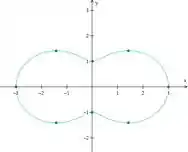
Esboce a curva e calcule a área limitada por ela
Passo 1
Olá, tudo bem?! Pronto para mais uma resolução?
Dada a curva parametrizada em coordenadas polares:
Devemos encontrar a área dessa curva a também desenhar um esboço dessa curva.
A área de uma curva em coordenadas polares é dada por:
Então temos que identificar cada termo dessa integral aí, substituir e calcular. O limite de integração é dado por todo o que nos permite varrer toda a figura, e assim calcular toda a sua área.
Passo 2
Primeiro vamos esboçar nossa curva, depois a gente calcula a área.
Para esboçar, vamos escolher alguns valores de dentro do intervalo e obter os valores de correspondentes. Assim a gente plota os pontos , depois liga.
Vamos fazer dessa forma manual porque nessa questão ele não pede para usar ferramenta gráfica, ok?
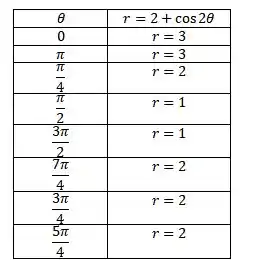
Plotando esses pontos e ligando tudo, vamos ter a curva:
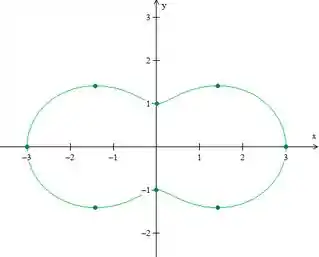
Agora sim vamos calcular a área da curva!
Passo 3
O limite de integração é dado por todo o que nos permite varrer toda a figura, e assim calcular toda a sua área.
Com esse intervalo conseguimos passar por todos os pontos da nossa figura.
Continuando, o é a própria parametrização:
Então é só substituir e integrar esse negócio.
Passo 4
Vamos lá:
Montando a integral:
Realizando o produto notável:
Utilizando da identidade trigonométrica :
Veja que as integrais que temos a fazer são tabeladas:
Realizando a distributiva do último termo:
Agora colocamos os limites de integração:
Resposta
