Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 16

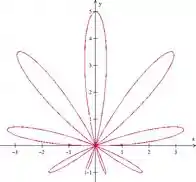
Trace a curva com uma ferramenta gráfica e calcule a área limitada por ela

r = 2 sen ⁡ θ + 3 sen ⁡ 9 θ

Passo 1

Olá, meu amigo, tudo bem?

Vou te ajudar a resolver essa atividade.

Dada a curva parametrizada:

r = 2 sen ⁡ θ + 3 sen ⁡ 9 θ

Queremos traçar o seu gráfico com ajuda de um software gráfico, e depois devemos calcular a área limitada por ela. Primeiro iremos traçar a curva, pois isso irá nos ajudar até no cálculo da área.

Para isso, vamos utilizar o Desmos, ele é gratuito e online, o que irá facilitar nossos trabalhos.

A área de uma curva em coordenadas polares é dada por:

A = ∫ a b 1 2 r 2 d θ

Então temos que identificar cada termo dessa integral aí, substituir e calcular.

Passo 2

Traçando a curva na ferramenta:

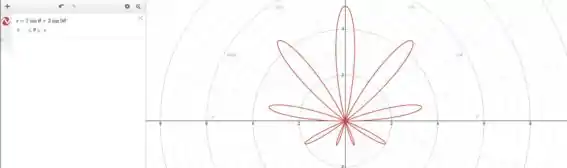
O intervalo de integração seria o intervalo em que a curva está definida:

a = 0

b = π

Veja que esse é o período da nossa curva, pois de 0 a π já é possível traçar toda a curva.

Ou seja, só metade do intervalo já é suficiente para traçar a curva.

Continuando, o r é a própria parametrização

r = 2 sen ⁡ θ + 3 sen ⁡ 9 θ

Então é só substituir e integrar esse negócio.

Passo 3

Vamos lá:

A = ∫ 0 π   1 2 r 2 d θ

Colocando a equação da nossa curva:

A = ∫ 0 π   1 2 ( 2 sin ⁡ θ + 3 sin ⁡ 9 θ ) 2 d θ

Realizando o produto notável:

A = ∫ 0 π   1 2 4 s i n 2 ⁡ θ + 12 s i n ⁡ θ s i n ⁡ 9 θ + 9 s i n 2 ⁡ 9 θ d θ

Colocando a relação do sin 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 :

A = ∫ 0 π   1 2 4 ⋅ 1 - c o s ⁡ 2 θ 2 + 12 s i n ⁡ θ s i n ⁡ 9 θ + 9 ⋅ 1 - c o s ⁡ 18 θ 2 d θ

Separando em diversas integrais:

A = ∫ 0 π   ( 1 - c o s ⁡ 2 θ ) d θ + 6 ∫ 0 π   s i n ⁡ θ s i n ⁡ 9 θ d θ + 9 4 ∫ 0 π   ( 1 - c o s ⁡ 18 θ ) d θ

A = 13 4 ∫ 0 π   d θ - ∫ 0 π   c o s ⁡ 2 θ d θ + 6 ∫ 0 π   1 2 ( c o s ⁡ 8 θ - c o s ⁡ 10 θ ) d θ - ∫ 0 π   c o s ⁡ 18 θ d θ

Calculando cada integral, lembre-se que aqui temos apenas integrais tabeladas:

A = 13 4 θ 0 π - 1 2 s i n ⁡ 2 θ 0 π + 3 1 8 s i n ⁡ 8 θ 0 π - 1 10 s i n ⁡ 10 θ 0 π - 1 18 s i n ⁡ 18 θ 0 π

Colocando os intervalos de integração:

A = 13 4 π - 1 2 sin ⁡ 2 π - sin ⁡ 0 + 3 1 8 sin ⁡ 8 π - sin ⁡ 0 - 1 10 sin ⁡ 10 π - sin ⁡ 0 - 1 18 sin ⁡ 18 π - sin ⁡ 0

Temos então:

A = 13 4 π

Resposta

A = 13 π 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região sombreada, onde r = θ .
Encontre a área da regiao sombreada, onde r = s e n (2 theta) .
Encontre a área da regiao que é limitada pelas curvas dadas e esta no setor especificado: r = e θ 2,π ≤ θ ≤ 2 π
Encontre a área da regiao que e limitada pelas curvas dadas e esta no setor especificado: r = θ 2,0 ≤ θ ≤ π / 4
Encontre a área da região que é limitada pelas curvas dadas e está no setor especificado: r = s e n ( θ ) ,π / 3 ≤ θ ≤ 2 π / 3