Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 29
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
Para resolver essa atividade eu vou utilizar o GeoGebra, para a gente visualizar melhor o que ocorre.
Depois que gerarmos esse gráfico, da mudança de variável, vamos passar a nossa curva que era em função de e para coordenadas cartesianas de fato, com a relação:
Passo 2
No Painel do GeoGebra, o que nós iremos fazer é plotar o gráfico dessa forma:
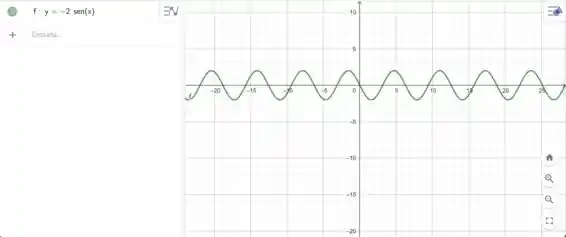
Agora a gente vai encontrar a equação da nossa figura de fato em coordenadas cartesianas.
Passo 3
A gente tem que:
Multiplicando ambos os lados por :
Lembre-se que:
E
Então:
Adicionando em ambos os lados da equação:
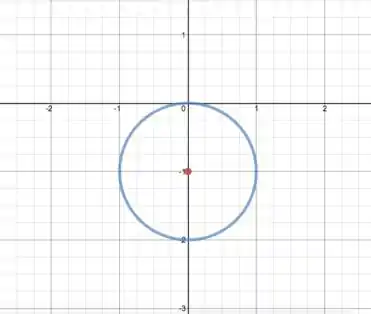
Temos então um círculo centrado em e raio . Podemos ver abaixo o gráfico da nossa figura:
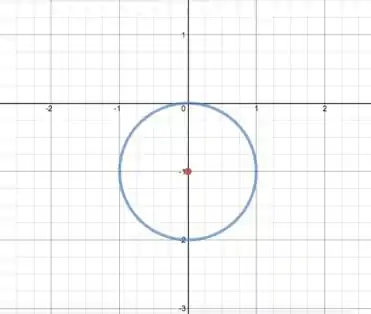
Resposta
