Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 17
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Olá, meu amigo. Temos aqui trabalhos a fazer.
Deveremos retirar a parametrização da nossa curva:
Isso é, deveremos colocar a equação em coordenadas cartesianas. Para isso, vamos utilizar da identidade trigonométrica:
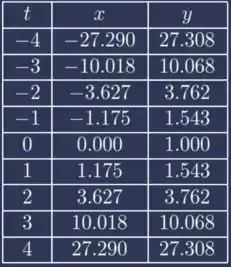
Para o gráfico, vamos fazer o seguinte, vamos criar uma tabela com valores de e plotar esses pontos num gráfico. Assim a gente tem o esboço do mesmo e a direção da curva quando o parâmetro cresce.
Passo 2
- Para “isolar” o parâmetro no caso em que temos seno hiperbólico e cosseno hiperbólico, usamos a relação fundamental da trigonometria:
- Criando nossa tabela com os valores de :
Assim
Que é a equação de uma hipérbole, “olhando” para o eixo , que é a variável que tá com sinal negativo.
Além disso, como
Sempre, para qualquer valor de , e
Então
Assim, estamos falando do ramo da hipérbole que está na parte positiva do eixo , com vértice no ponto .
Passo 3
Traçando nossa curva, temos
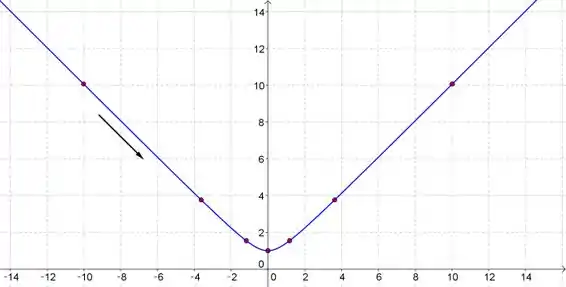
Para o comportamento do gráfico, basta que a gente veja a tabela, à medida que cresce a gente tem que também cresce.
Resposta
