Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 8.1 - Ex. 31
Esboce a curva com a equação e usa a simetria para achar seu comprimento.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o esboço da curva e usar a simetria dela para achar o seu comprimento.
Bom, o esboço dessa curva será o seguinte:
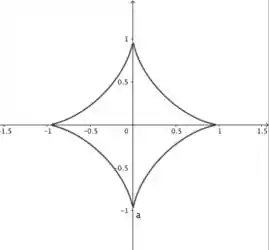
Perceba que ela é simétrica em relação aos eixos e . Agora para achar seu comprimento, vamos usar a fórmula do comprimento de arco:
Vamos lá!
Passo 2
Para calcular o comprimento, a primeira coisa a se fazer é lembrar a fórmula que calcula o comprimento de uma curva em um intervalo .
Essa é a fórmula. E perceba que como a nossa figura é simétrica, podemos calcular o comprimento do primeiro quadrante e multiplicar por . O intervalo de integração será então e a função será dependente dos valores de .
Mas antes, vamos isolar o na equação da curva:
Logo, temos:
Passo 3
Precisamos de e do intervalo de integração para montar a integral. Se , então derivando, temos:
Colocando em evidência:
Como a nossa fórmula do comprimento de arco, tem derivada ao quadrado, vamos elevar os dois lados da equação ao quadrado para obter:
Passo 4
Já o intervalo de integração será de até .
Sendo assim, o comprimento será dado por:
Simplificando:
Passo 5
Dessa forma, integrando, temos:
Calculando as somas:
Simplificando:
E aplicando os limites de integração, temos:
Sendo assim, o comprimento será .
Valeu, galera! Até a próxima! 😉