Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 1c
Desenhe a curva dada (coordenadas polares)
c)
Passo 1
Neste caso, vamos isolar ρ e comparar com as outras equações paramétricas conhecidas para maior entendimento deste gráfico!
Contudo, lembre que :
Substituindo teremos que:
Passo 2
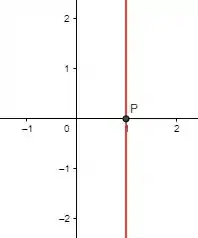
Descobrimos então que neste caso x é constante, logo nosso gráfico devera ser uma reta vertical que corta o horizontal no ponto 1!
Resposta
Exercícios de Livros Relacionados
7. y = 1 2 e x + e - xd e0,1a( 1 , e x + e - 1 2 )
6. x = 1 3 y 3 + 1 4 y ,1 ≤ y≤ 3
12. y = 6 ( x 2 3 - 1 )d eP 0 1 , 0a t éP 1 ( 2 √ 2 , 6 ) é .
Calcule o comprimento de arco da curva dada na forma paramétrica. x = e t cos t y = e t s e nt,1 ≤ t ≤ 2
Calcule o comprimento de arco da curva dada na forma paramétrica. x = - s e nt y = cos t,t ∈ [ 0 , 2 π ]