Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 1b
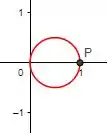
Desenhe a curva dada (coordenadas polares)
b)
Passo 1
Tomando a função dada no enunciado e multiplicando por ρ nos dois lados:
Contundo, devemos lembrar que:
Substituindo, teremos:
Ou seja, se trata de um circulo!
Passo 2
Agora para termos uma noção de onde esse circulo se situa vamos jogar alguns valores para θ:
Isso significa que o diâmetro do nosso circulo está deitado no segmento que vai de 0 a 1:
Resposta
Exercícios de Livros Relacionados
Estabeleça a integral que dá o comprimento de arco da curva dada. y = s e n3 x , 0 ≤ x ≤ 2 π
Calcule o comprimento de arco da curva dada na forma paramétrica. x = 3 t + 2 y = t - 1,t ∈ [ 0 , 2 ]
Calcule o comprimento de arco da curva dada na forma paramétrica. x = ts e nt y = t cos t,t ∈ [ 0 , π ]
Calcule o comprimento de arco da curva dada na forma paramétrica. x = t 3 y = t 2,1 ≤ t ≤ 3
Calcule o comprimento de arco da curva dada na forma paramétrica. x = 2 cos t + 2 ts e nt y = 2 s e nt - 2 t cos t,0 ≤ t ≤ π 2