Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 113
Para , esboce a curva que tem e . O que se pode dizer sobre a concavidade dessa curva? Justifique sua resposta.
Passo 1
A função que apresenta é a logaritmo natural...
Vamos então analisar o gráfico de para :
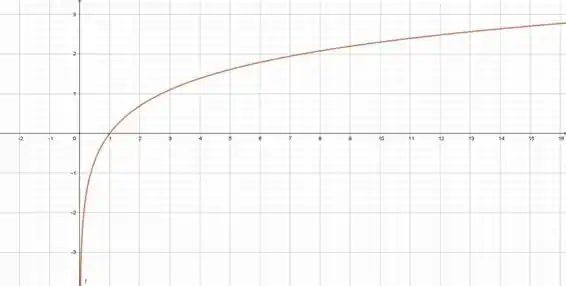
Vemos pelo gráfico que a concavidade é sempre para baixo...
Mas por quê?
A concavidade é dada pela derivada segunda né? Vamos ver então...
Passo 2
A derivada segunda da função é:
Veja que é sempre positivo, mas é sempre negativo, logo, independente de qual seja o valor de x, . Portanto, a concavidade é sempre para baixo.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o roteiro desta seção para esboçar a curva y = x 2 - 1 2 3
Use o roteiro desta seção para esboçar a curva y = x e - x
Use o roteiro desta seção para esboçar a curva y = x + x
Use o roteiro desta seção para esboçar a curva y = x 2 + 1 - x
Use o roteiro desta seção para esboçar a curva y = x ln x 2