Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 106
Esboce o gráfico de uma função duas vezes derivável que passe pelos pontos e cujas duas primeiras derivadas tenham a seguinte distribuição de sinais:
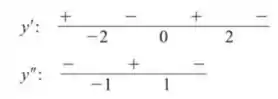
Passo 1
Sabemos que:
- se a função é crescente em x.
- se a função é decrescente em x.
- se x é um ponto crítico no gráfico (máximo ou mínimo absolutos)
- se a concavidade do gráfico é para cima em x.
- se a concavidade do gráfico é para baixo em x.
- se x é um ponto de inflexão (onde muda a concavidade)
A partir dessas informações, podemos esboçar a curva:
Passo 2
Primeiramente, marque os pontos dados: .
Perceba que a função é simétrica em relação ao eixo y.
Veja que a função é crescente no intervalo e e decrescente em e
Agora, vemos também que concavidade é para baixo em , para cima em e para baixo novamente em . Ou seja, temos pontos de inflexão nas coordenadas e .
Passo 3
Juntando essas informações, podemos esboçar o gráfico:
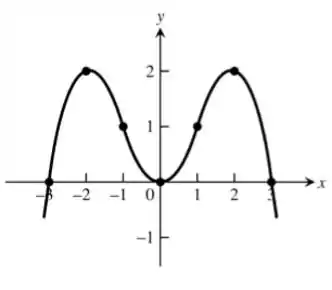
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine os valores das constantes a ,b e c , de modo que o gráfico de y = a x 3 + b x 2 + c x tenha um máximo local em x = 3 , um mínimo local em x = - 1 e um ponto de inflexão em ( 1 ,11 ) .
Determine os valores das constantes a ,b e c , de modo que o gráfico de y = x 2 + a ( b x + c ) tenha um mínimo local em x = 3 , um mínimo local em - 1 , - 2 .
Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflex
Esboce o gráfico da função racional: y = x - 1 x 2 ( x - 2 )
Nos Exercícios de 13 a 32, faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos de f ; os pontos de inflexão do gráfico de f ; os intervalos nos quais f