Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 7
Identifique os pontos de inflexão e os máximos e mínimos locais da função representada graficamente. Identifique os intervalos em que a função é côncava para cima e aqueles em que ela é côncava para baixo.
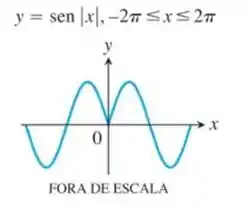
Passo 1
Nessa função, como temos módulo na função, vamos analisar dois casos separadamente:
- 1: Caso
- 2: Caso
Nesse caso, nossa função se resume a .
Nesse caso, nossa função fica: (a função seno é ímpar).
(Veja que esses dois casos formam o gráfico completo, um do lado esquerdo da origem e outro do lado direito).
Vamos calcular a derivada primeira e segunda em ambos os casos:
1: e
2: e
Passo 2
Vamos encontrar os pontos críticos agora, que são onde a derivada é zero.
Vamos ver se são pontos de máximo ou mínimo pela derivada segunda:
Então a função possui pontos de máximo em e pontos de mínimo em .
Passo 3
Os pontos de inflexão são onde muda a concavidade, então vamos ver em que pontos a derivada segunda é positiva ou negativa...
Temos que
Então, temos que a concavidade é para baixo em e e para cima em e .
E os pontos de inflexão são: e .
Resposta
Pontos de máximo em e pontos de mínimo em .
A concavidade é para baixo em e e para cima em e .
E os pontos de inflexão são: e .