Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.2 - Ex. 1b

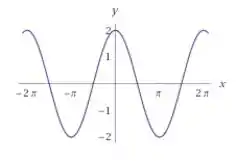
Esboce o gráfico.

y = 2 cos x

Passo 1

Para esboçar esse gráfico devemos lembrar da função cos x que possiu os valores:

cos 0 = 1

cos ((pi)/(2)) = 0

cos (pi) = - 1

cos (- (pi)/(2)) = 0

E assim por diante.

Passo 2

Como a função f (x) = 2 cos x tem um dois multiplicando a função cosseno, os valores serão multiplicado por 2 , ficando assim:

2 * cos (0) = 2 * 1 = 2 -> (0,2)

2 * cos ((pi)/(2)) = 2 * 0 = 0 -> ((pi)/(2) , 0)

2 * cos (pi) = 2 * (- 1) = - 2 -> (pi , - 2)

2 * cos ((3 pi)/(2)) = 2 * 0 = 0 -> ((3 pi)/(2) , 0)

2 * cos (- (pi)/(2)) = 2 * 0 = 0 -> (- (pi)/(2) , 0)

2 * cos (- pi) = 2 * (- 1) = - 2 -> (- pi , - 2)

2 * cos (- (3 pi)/(2)) = 2 * 0 = 0 -> (- (3 pi)/(2) , 0)

Assim podemos esboçar o gráfico:

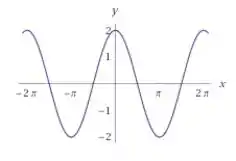
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache todos os valores de t no intervalo de 0,2 π para os quais a equação dada é satisfeita:c) t gt =- 3
Ache todos os valores de t no intervalo de 0,2 π para os quais a equação dada é satisfeita:f) c o s e ct =2
Use as fórmulas para adição para deduzir as identidades nos Exercicios 31-36.32. cos ⁡ x + π 2 = - s e n x
Use as fórmulas para adição para deduzir as identidades nos Exercicios 31-36.33. s en ⁡ x + π 2 = cos ⁡ ( x )
Use as fórmulas para adição para deduzir as identidades nos Exercicios 31-36.34. sen ⁡ x - π 2 = - cos ⁡ ( x )