Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.2 - Ex. 16
Use um sistema de computação algébrica para desenhar um campo de direções para a equação diferencial dada. Obtenha uma impressão e esboce uma curva solução que passe por (0, 1). Use o SCA para desenhar a curva solução e compare o resultado com seu esboço.
Passo 1
Utilizando um sistema de computação algébrica obtemos o seguinte campo de direção:
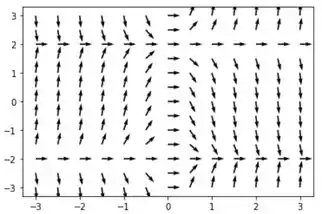
Passo 2
As curvas soluções são curvas ques respeitam as inclinações e acompanham o campo de direção.
Então a curva que passa pelo ponto é:
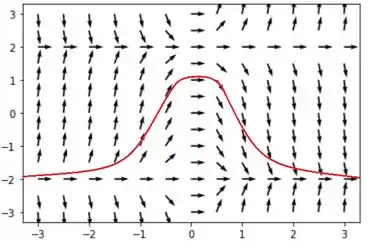
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Ache uma solução da equação diferencial que satisfaça a condição dada. x d y d x = 2 y + 4 x 2 ln x ; y = 4 quando x = 1 .
Ache uma solução da equação diferencial que satisfaça a condição dada. d y d x = 1 + 2 y cotg x ; y = 2 quando x = 1 4 π .
Os Exercícios de 75 a 81 pertencem à Secção Suplementar 7.8. Nos Exercícios 75 e 76, ache a solução completa da equação diferencial. 75 )x ² . d y d x + 2 x y = 3 x ² + 1 ² ²
Nos Exercícios 77 e 78, ache uma solução da equação diferencial, que satisfaça a condição dada. 77 ) cos x . d y d x = 1 - y - s e nx ; y = 2q u a n d ox = 0 .
Os Exercícios de 75 a 81 pertencem à Secção Suplementar 7.8. Nos Exercícios 75 e 76, ache a solução completa da equação diferencial. 76 ) d x d y + 2 x . c o t gy = s e c ²y ²