Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.2 - Ex. 16
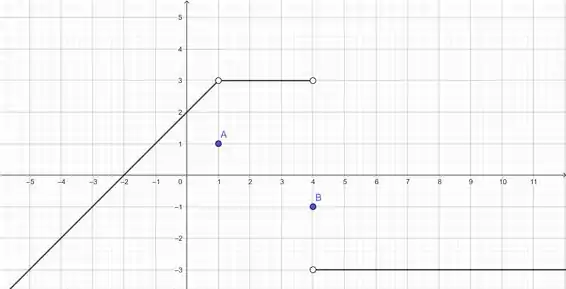
Esboce o gráfico de um exemplo de função que satisfaça todas as condições dadas.
Passo 1
Olá, meu caro estudante. Pronto para mais uma resolução?
Aqui a gente vai gerar um gráfico de uma função dada, que deve satisfazer todas as condições dadas.
Precisamos prestar atenção em relação aos limites laterais e também nos pontos de definição da função, que podem ser diferentes dos pontos de limite da função.
Então, pessoal, uma dica para esse tipo de questão é: comece sempre marcando no gráfico a bolinha cheia onde você a sabe que a função é definida naquele ponto.
Neste caso, a gente começa marcando onde estão: e.
Feito isso, a gente olha para os limites! Aí é só desenha uma função que leve para onde o limite indica, mas marca-la com a bolinha vazia, caso a função exista em outro ponto.
Vamos lá!
Passo 2
Primeiro vamos marcar os pontos:
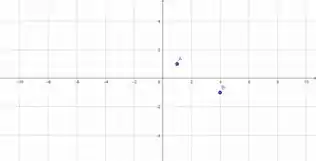
Agora vamos ao limite lateral:
Sendo assim, quando estamos nos aproximando de pela direita, nossa função tenderá a :
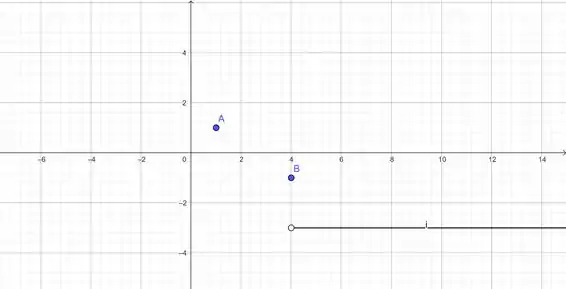
Agora vamos ao limite lateral:
Sendo assim, nos aproximando de pela esquerda, nossa função tenderá a :
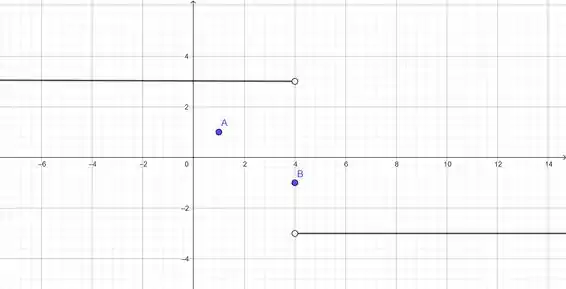
E agora por último, mas não menos importante, , onde nos aproximando de tanto pela esquerda quanto pela direita, deveremos ter
É isso meu amigo, construímos esse belo gráfico da nossa função. Forte abraço e até uma próxima.
Resposta
