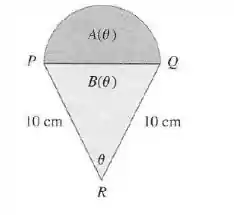
O semicírculo com diâmetro está sobre um triangulo isósceles para formar uma região com um formato de sorvete, conforme mostra a figura. Se for a área do semicírculo e a área do triângulo, encontre
Passo 1
E ai galerinha, bora resolver essa questãozinha
Mas vamos fazer de um jeito diferente, antes de substituir todos os valores, vamos resolver ela por teoria, e depois vemos na prática como de fato ela ficará, ok?
Para resolver esse problema, primeiro precisamos encontrar as fórmulas para as áreas do semicírculo e do triângulo em termos de θ, e então calcular o limite conforme θ se aproxima de
Dado que o semicírculo tem diâmetro , seu raio é metade do comprimento do segmento , que podemos chamar de ., como mostra a imagem dada no enunciado
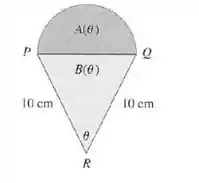
Portanto, o raio do semicírculo é .
A área de um semicírculo é dada por:
Substituindo o raio pelo valor encontrado, temos:
Passo 2
Para o triângulo isósceles , como é um triângulo isósceles, podemos dividir o triângulo em dois triângulos retângulos idênticos e calcular a área de um deles.
Seja a altura do triângulo (que é a distância do ponto médio de ao vértice ).
A área do triângulo é dada por:
Para encontrar a base do triângulo, precisamos usar um pouco de trigonometria.
Passo 3
Seja o ângulo entre .
Como o triângulo é isósceles, temos:
Podemos usar o cosseno do ângulo para encontrar a base:
Portanto, a área do triângulo é:
Passo 4
Agora, para calcular o limite precisamos substituir as expressões que encontramos para e e então calcular o limite:
Sabemos que , então:
Portanto, esse é o valor do limite.
Passo 5
Agora vamos aplicar na pratica todo o nosso conhecimento obtido dos passos anteriores, portanto a atividade nos pede para encontrarmos primeiramente a área do triangulo e do semicírculo do nosso ‘sorvete’ e após isso calcular o limite de seu consciente.
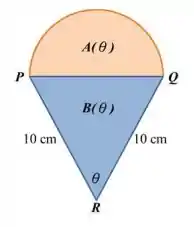
A área de um triângulo é dada por:
E a área de uma semicircunferência:
Então primeiramente, devemos relacionar e com .
Passo 6
é a área do semicírculo cujo raio é a metade do segmento :
O segmento tem o comprimento de:
Então o raio do semicírculo fica:
E área vai ser:
Passo 7
é a área do triângulo cuja altura é a distância do ponto até o ponto médio do segmento :
Então a área fica assim:
Passo 8
Então, a razão entre as áreas é:
Logo: