Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 5
Esboce o gráfico de uma função para a qual , , se e se .
Passo 1
Vamos analisar as informações para esboçar o gráfico.
Primeiro temos um ponto da função:
Temos que a derivada em é zero, o que nos diz que nesse ponto a inclinação é zero, a reta tangente nesse ponto é horizontal.
Passo 2
Temos também que para valores menores de zero as inclinações são decrescentes à medida que aumenta.
E por último, para valores maiores de zero as inclinações são também crescentes à medida que aumenta.
Passo 3
Agora vamos esboçar, a função se encaixa em todas as condições:
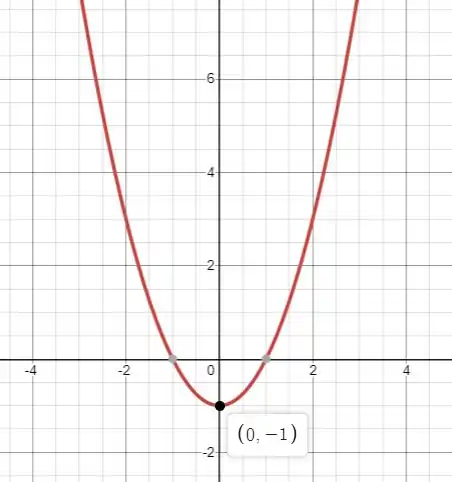
Resposta
Exercícios de Livros Relacionados
Determine todos os pontos x , y no gráfico de g x = 1 3 x 3 - 3 2 x 2 + 1 com tangentes paralelas à reta 8 x - 2 y = 1 .
Tangentes horizontais Determine equações para as tangentes horizontais à curva y = x 3 - 3 x - 2 . Também determine equações para as retas que são perpendiculares a essas tangentes nos pontos de tangê
O polinômio geral de grau n tem a forma P x = a n x n + a n - 1 x n - 1 + … + a 2 x 2 + a 1 x + a 0 Em que a n ≠ 0 . Determine P ' x .
Determine todos os pontos x , y no gráfico de f x = x 2 com tangentes que passam pelo ponto ( 3,8 ) .
Para os Exercícios 67 e 68, avalie cada limite ao converter cada um deles em uma derivada com um determinado valor de x . lim x → - 1 x 2 / 9 - 1 x - 1