Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.1 - Ex. 26
Esboce o gráfico da função:
Passo 1
Eaee, tudo bem?? Bom... queremos esboçar o gráfico da seguinte função:
Para isso, precisamos saber que a função está na forma:
Precisamos saber também que, como trata-se de uma função linear de duas variáveis, o gráfico desse tipo de função é um plano no espaço tridimensional.
Além disso, devemos igualar cada variável a zero separadamente e analisar como seria a figura no plano 2D. Com isso, poderemos observar vistas 2D e plotar a figura tridimensional em seguida.
Agora bora lá!! 😉
Passo 2
Com base no passo 1, podemos afirmar que:
É o mesmo que:
Agora vamos igualar cada variável a zero e analisar o resultado.
No plano :
Percebemos que trata-se de uma circunferência de raio .
No plano
Ou seja, trata-se de uma parábola.
No plano
Ou seja, trata-se de uma parábola.
Com isso, podemos concluir que é a equação de um paraboloide circular de vértice .
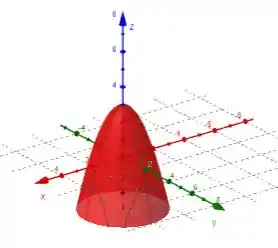
Resposta
