Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 65
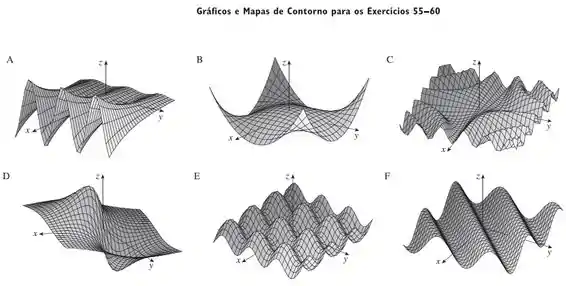
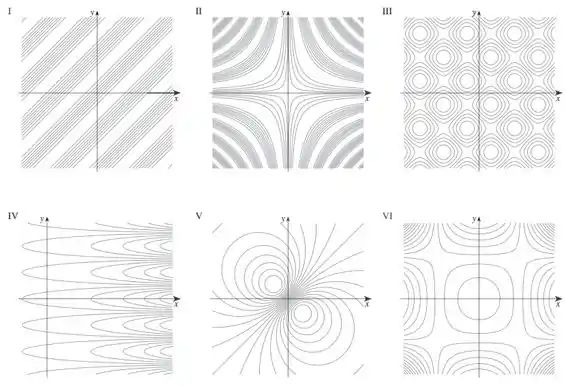
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha.
Passo 1
Olá, meu bom e velho amigo. Vamos resolver essa atividade, irei te ajudar a entender o que está acontecendo aqui e como prosseguir.
Temos então a função:
E queremos relacionar qual o gráfico dessa função e qual sua curva de nível, dentre as várias opções que nos foram dadas.
Para escolhermos corretamente qual o gráfico tridimensional dessa função, deveremos analisar o comportamento da mesma em determinados pontos, isso nos dará algumas dicas.
Poderemos analisar o comportamento da função próxima a origem, assim como deveremos também analisar o que ocorre na própria origem.
Deveremos analisar também o que ocorre quando estamos perto dos eixos ordenados.
Passo 2
(a) Pensando só na parte próximo da origem a função vale e vai diminuindo para ambos os lados, zera em e e continua diminuindo pra valores negativos. Para temos a mesma coisa, mas no eixo .
Próximo dos eixos uma das partes vai tender a valer e a outra parte vai fazer ficar negativo, com ressalva a pontos próximos a origem. Se pensarmos em pontos onde tanto tanto são grandes o suficiente para negativar as duas partes, então na multiplicação fica positivo e aumentando.
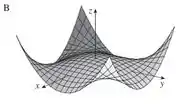
Um outro ponto a se analisar é que se traçarmos essa função no plano temos que ela é uma parábola:
E se traçarmos no plano temos outra parábola:
O gráfico que representa esse comportamento é o B.
Passo 3
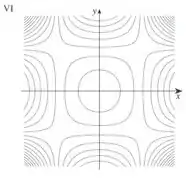
(b) Se repararmos, a função é igual a zero ao longo das linhas e e analisando o gráfico B, se fizéssemos cortes na função a uma altura constante, as curvas que apareceriam seriam as do número VI.
Resposta
- B
- VI