Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 64
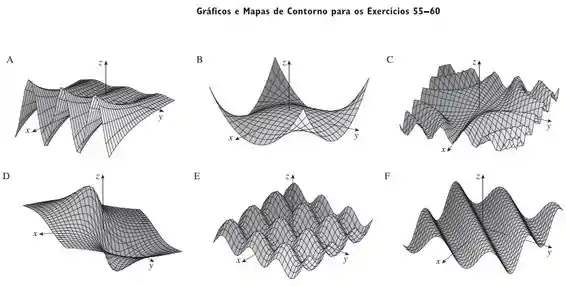
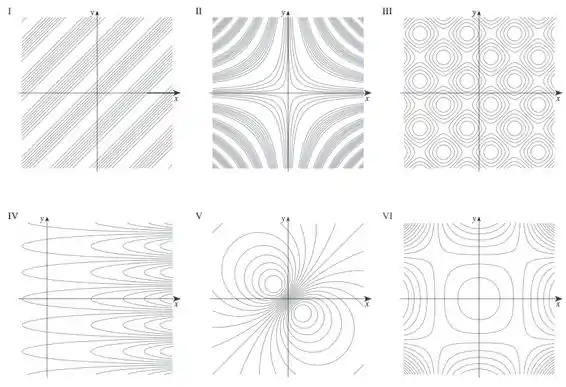
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha.
Passo 1
Olá, meu bom e velho amigo. Vamos resolver essa atividade, irei te ajudar a entender o que está acontecendo aqui e como prosseguir.
Temos então a função:
E queremos relacionar qual o gráfico dessa função e qual sua curva de nível, dentre as várias opções que nos foram dadas.
Para escolhermos corretamente qual o gráfico tridimensional dessa função, deveremos analisar o comportamento da mesma em determinados pontos, isso nos dará algumas dicas.
É interessante lembrar que a função seno é periódica, e que seu comportamento oscila como uma onda.
Passo 2
- Com a soma de dois senos, que dependem de variáveis diferentes, o que esperamos são várias ondas no gráfico.
- Como há várias ondas senoidais por toda parte, o contorno deve se assemelhar a um monte de corcovas. Assim como em um mapa de uma cordilheira.
Quando , que é o ponto em que a curva encontra o plano , nós temos , uma curva senoidal que já conhecemos.
Quando , que é o ponto em que a curva encontra o plano , nós temos , uma curva senoidal que já conhecemos.
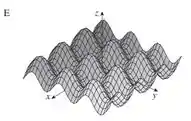
O gráfico que representa esse comportamento é o E.
Passo 3
E como as curvas de pecado estão espalhadas igualmente ao redor, o mapa de contorno deve refletir isso.
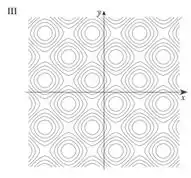
Analisando o gráfico F, se fizéssemos cortes na função a uma altura constante, as curvas que apareceriam seriam as do número III.
Resposta
- E
- III