Utilize um computador para traçar o gráfico da função, usando vários pontos de vista e tamanhos de janela. Comente o comportamento da função no limite. O que acontece quando e se tornam muito grandes? O que acontece quando se aproxima da origem?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos traçar o seu gráfico em vários pontos de vista para podermos comentar sobre o o comportamento da função nos limites:
Agora bora lá!! 😉
Passo 2
Utilizando uma ferramenta gráfica para plotar o gráfico em algumas perspectivas e janelas, temos:
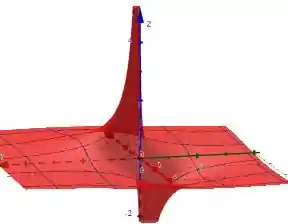
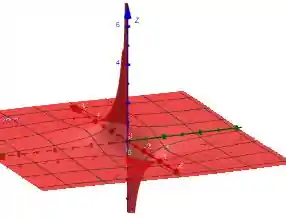
Agora vamos analisar os limites!!
Passo 3
Agora vamos analisar com o seguinte limite:
Quando uma das variáveis a função tende a zero, ou seja, .
Isso acontece porque o grau do denominador é maior, fazendo o denominador “crescer mais rápido”.
Passo 4
Agora vamos analisar com o seguinte limite:
Quando a função de aproxima da origem temos que , e na origem parece que a função não tem um limite, uma vez que de diversos pontos diferentes, temos que a altura com que nos aproximamos seja diferente.
Resposta
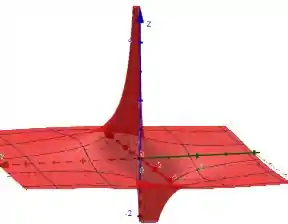
Quando uma das variáveis a função tende a zero, ou seja, .
Quando uma das variáveis a função tende a infinito, ou seja, .