Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 66
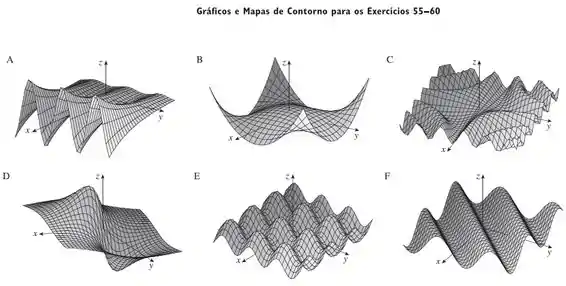
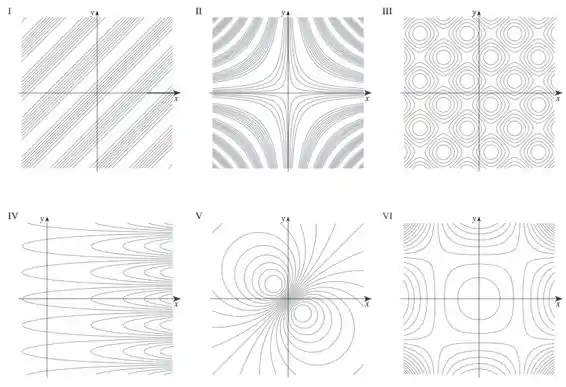
Faça uma correspondência entre a função (a) e seu gráfico (indicado por A-F na página 828), (b) e seus mapas de contorno (indicado por I-VI). Justifique sua escolha.
Passo 1
Olá, meu bom e velho amigo. Vamos resolver essa atividade, irei te ajudar a entender o que está acontecendo aqui e como prosseguir.
Temos então a função:
E queremos relacionar qual o gráfico dessa função e qual sua curva de nível, dentre as várias opções que nos foram dadas.
Para encontrarmos o gráfico da função, não tem muitos segredos, vamos ter que analisar alguns pontos e comportamentos importantes da função. Iremos analisar por exemplo o que acontece quando ou tende ao infinito.
Podemos analisar também o que acontece na origem, o que acontece quando , ou . Enfim, deveremos analisar como se comporta a nossa função e ir comparando com os gráficos que temos ali a fim de excluir alguns e selecionar outros até podermos fazer a escolha.
Passo 2
(a) Para ambas as variáveis, temos que o grau no denominador é maior que no numerador, então se pensarmos quando uma das variáveis teremos que .
Como o denominador é sempre positivo, vamos olhar para o numerador.
No numerador temos que na reta a função zera, quando vamos para a função aumenta e vai ter um pico até que uma das variáveis seja suficientemente grande ou pequena, para que a função diminua para .
Quando teremos um vale pico até que uma das variáveis seja suficientemente grande ou pequena, para que a função diminua para .
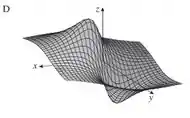
O gráfico que representa esse comportamento é o D.
Passo 3
(b) A curva de nível da nossa função:
São da seguinte forma:
Em que é uma constante:
Substituindo por uma constante :
Passando todo mundo para o mesmo lado:
Completando os quadrados:
Colocando em forma de produtos notáveis:
Note que essa equação representa um círculo com centro em . Isso significa que os centros dos círculos estão na linha .
Analisando o gráfico D e as nossas analises matemáticas, se fizéssemos cortes na função a uma altura constante, as curvas que apareceriam seriam as do número V.
Resposta
- D
- V