Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 73
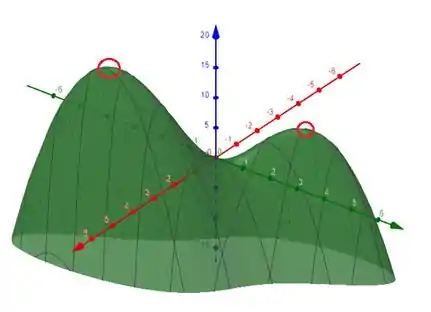
Utilize um computador para traçar o gráfico da função, utilizando vários pontos de vista e tamanhos de janela. Imprima aquela que apresente melhor os “picos e vales”. Você acha que essa função tem um valor máximo? Você poderia identificar os pontos do gráfico correspondentes aos “máximos locais”? E aos “mínimos locais”?
Passo 1
Olá, meu brother estudante. Vamos aprender um pouco hoje!!
A gente tem a função:
E iremos produzir seu gráfico utilizando um software gráfico. Devemos também discutir sobre o valor máximo dessa função, além de identificar os máximos locais e mínimos locais.
Máximos e mínimos locais são pontos em um gráfico de uma função onde a função atinge valores máximos ou mínimos em relação aos pontos próximos a eles. Os máximos e mínimos locais são relativos aos pontos próximos, enquanto os globais são relativos a todo o domínio da função.
Então iremos plotar o gráfico dessa função utilizando o GeoGebra, por ser um software gráfico gratuito e online.
Nele iremos analisar os picos e vales da nossa função, e iremos analisar se o comportamento do gráfico da função permite crescimentos e decrescimentos após os picos e vales que encontrarmos.
Passo 2
Traçando o gráfico e analisando diversos ângulos,
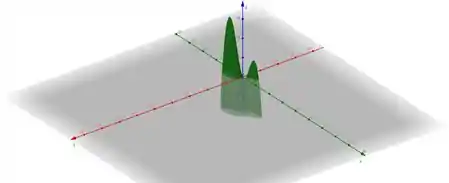
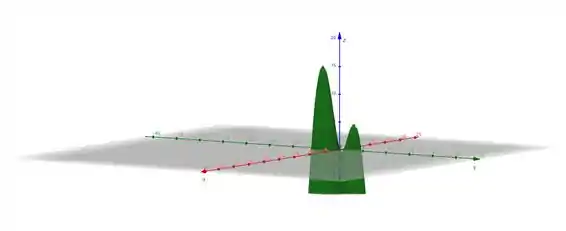
o que melhor representa os máximos da função é:
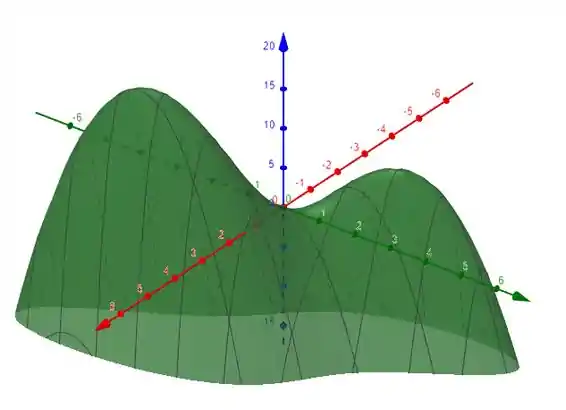
Pois conseguimos visualizar melhor os picos da nossa função, e também seu comportamento de decrescimento em .
Passo 3
Podemos claramente indicar que os picos, ou máximos locais, da função que são esses dois
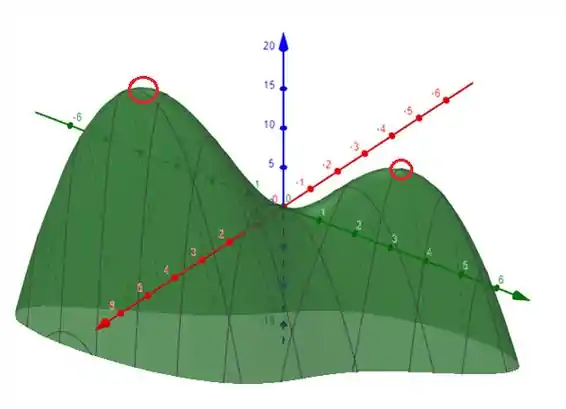
Já para mínimos, não temos nenhum ponto nessa função. Já que podemos ver que ela aparenta decrescer indefinidamente.
Resposta
