Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.2 - Ex. 1g

Esboce o gráfico da função F dada por

F (x) = int_0^x e^(- |t|) d t

Passo 1

A questão quer que esbocemos o gráfico de F ( x ) que é função dada por uma integral. Para isso, vamos tentar achar uma expressão fechada para ela.

Aqui temos que tomar cuidado antes de integrar. Lembre-se que

|t| = {[[- t , t < 0],[t , t >= 0]])

Assim, vamos supor primeiro x >= 0 , de modo que no intervalo [ 0 , x ] temos que e^(- |t|) = e^(- t) . Portanto,

F (x) = int_0^x e^(- t) d t = (- e^(- t))_0^x = 1 - e^(- x)

Já para x < 0 , temos que e^(- |t|) = e^t . Assim,

F (x) = int_0^x e^t d t = e^x - 1

Desta forma,

F (x) = {[[e^x - 1 , x < 0],[1 - e^(- x) , x >= 0]])

Passo 2

Um esboço da curva é dado a seguir:

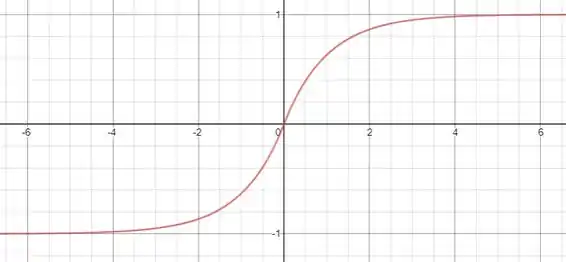
Note que a função é ímpar e contínua!

Resposta

Esboço de gráfico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada item, tente calcular exatamente a integral com um CAS. Se sua resposta não for numericamente simples, então use o CAS para encontrar uma aproximação numérica da integral. ∫ 0 + ∞ 1 1 + x 3 d x
Expresse a integral imprópria como um limite e, então, calcule esse limite com um CAS. Confirme sua resposta calculando diretamente as integrais com um CAS. ∫ 0 + ∞ e - x cos ⁡ x d x
Em cada item, confirme o resultado com um CAS. ∫ - ∞ + ∞ e - x 2 d x = π
Em cada parte, use o Exercício 52 para determinar se a integral converge ou diverge. Se convergir, então use a parte (b) daquele exercício para encontrar uma cota superior para o valor da integral. (a
Em cada parte, use o Exercício 52 para determinar se a integral converge ou diverge. Se convergir, então use a parte (b) daquele exercício para encontrar uma cota superior para o valor da integral. (a