(a) Esboce o gráfico da função dada por três períodos.
(b) Encontre a série de Fourier para a equação dada.
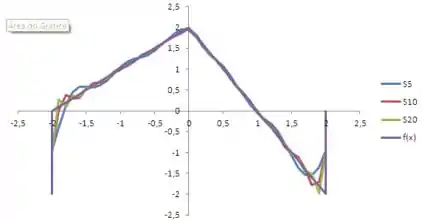
(c) Faça o gráfico da soma parcial em função de para 5, 10 e 20.
(d) Descreva como a série de Fourier parece estar convergindo.
Passo 1
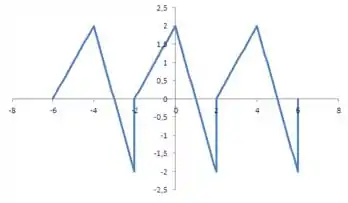
O item (a) nos pede para desenhar o gráfico da função. A nossa função é para o intervalo e para . O que vamos fazer é esboçar a função para este período e estendê-la para um perído anterior e para o perído seguinte. Ficamos então com algo da forma:
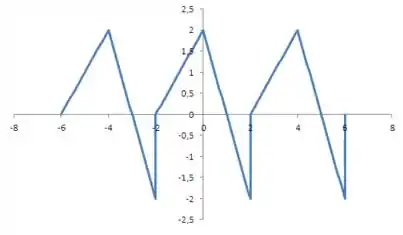
Passo 2
Vamos agora para o item (b). Ele nos pede para encontrar a série de Fourier para a função . A série de Fourier é uma equação da forma:
Precisamos então obter os termos e . O intervalo de uma função escrita como série de Fourier é definido como . Então, para a nossa função . Tudo bem?
O próximo passo é o cálculo dos coeficientes. O coeficiente é definido por:
Agora vamos determinar :
Por fim, vamos calcular :
Aplicando na função:
A soma é zero para par e 2 para ímpar. Então, para o somatório da parte cosseno apenas interessam os valores de ímpar. Certo?
Então, para a parte cosseno vamos substituir e por , para assegurar que apenas serão contabilizados os valores ímpares de . Ficamos então com:
Como só possui valor para par e para ímpar vamos reescrevê-lo como:
Então
Passo 3
Vamos agora para o item (c). Ele nos pede para montar os gráficos de para 5, 10 e 20 termos. Com o auxílio de Excel podemos montar o somatório para , 10 e 20. A seguir são mostrados os gráficos das somas e da função:
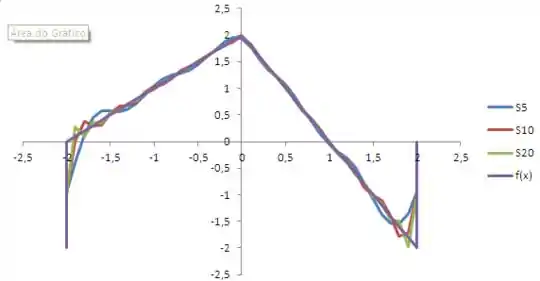
Vamos agora responder o item (d). A partir da análise do gráfico podemos ver que a série de Fourier converge para a função . Alternativamente podemos verificar que os valores de e decrescem com o aumento de :
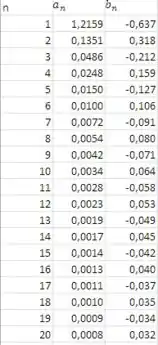
Como isso acontece, o esperado é que para , , e por isso, para um suficientemente grande, o valor do somatório deve convergir para um valor único.
Resposta
(a)
(b)
(c)