Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.2 - Ex. 10

Se f x = x + 1 ,   s e - 1 < x < 0 x ,   s e   0 < x < 1 se f x + 2 = f ( x ) , encontre uma fórmula para f ( x ) no intervalo 1 < x < 2 e no intervalo 8 < x < 9 .

Passo 1

Vamos começar olhando o gráfico da função dada (basta jogar em um CAS, como é o caso do DESMOS e Symbolab), com o seguinte comando:

{ - 1 < x < 0 : x + 1 ;   0 < x < 1 : x }

Observando o comportamento:

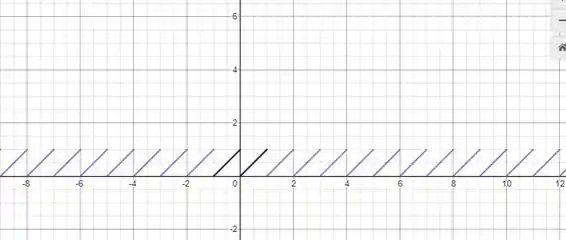
Aplicando os valores dos intervalos nas condições dadas:

f x = x + 1 ,   s e - 1 < x < 0 x ,   s e   0 < x < 1

[Lembre-se de que uma linha que passa pelos pontos ( x 1 ,   y 1 ) e ( x 2 ,   y 2 ) é dada por :

y - y 1 =   y 2 - y 1 x 2 - x 1 .   ( x - x 1 )

Podemos ver que para 1   < x   < 2 . Então   f   ( x ) é uma linha entre ( 1,0 ) e ( 2,1 ) . A equação desta linha é:

y - 0 =   1 - 0 2 - 1 .   x - 1

y = x - 1

f   ( x )   =   x - 1 ,   1   < x   < 2

Para 8   < x   < 9 . Então, f   ( x ) é uma linha entre ( 8,0 ) e ( 9,1 ) . Portanto:

y - 0 =   1 - 0 9 - 8 .   x - 8

y = x - 8

f   ( x )   =   x - 8 ,   8   < x   < 9

Resposta

f   ( x )   =   x - 1 ,   1   < x   < 2

f   ( x )   =   x - 8 ,   8   < x   < 9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. s en ⁡ π x / L
Verifique as Eqs. (6) e (7) nessa seção integrando diretamente.
Se f ( x )=L–x para 0x 2 L e se f ( x + 2 L )=f ( x ) , encontre uma fórmula para f ( x ) no intervalo – L x0 .
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. tan ⁡ π x
Em cada um dos problemas de 1 a 8, determine se a função dada é periódica. Se for, encontre seu período fundamental. f x = 0 , 2 n - 1 ≤ x2 n 1 , 2 n ≤ x2 n + 1n = 0 , ± 1 , ± 2 …