Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 1d
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua.
Passo 1
Nesse caso, à esquerda de temos uma parábola e à direita de temos uma reta:
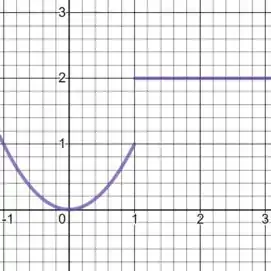
Podemos percorrer toda a curva de sem saltos, exceto no ponto . Então, por termos um “salto” em , dizemos que a função é continua em todo real exceto em .
é contínua para todo .
Resposta
é contínua para todo .
Exercícios de Livros Relacionados
Se as funçõesf ( x ) e g ( x ) são contínuas para 0 ≤ x ≤ 1 , f x g x poderia ser descontínua em um ponto de [ 0 ,1 ] ? Justifique sua resposta.
Use o exercício 69 juntamente com as identidades s e n h + c = s e nh cos c + cos hs e nc ; c o s h + c = c o sh cos c - s e nhs e nc ; Para provar que tanto f ( x ) = s e n ( x ) e g x = c o s
Dê um exemplo de funções f eg , ambas contínuas em x=0, para as quais a composta f o g seja descontínua em x = 0 . Isso contradiz o Teorema 9 (Se f é contínua em c e g é contínua em f(c), então a comp
Uma função descontínua em todos os pontosUse o fato de que todo intervalo não vazio de números reais contém tanto números racionais quanto irracionais para mostrar que a função f x = 1 , s exér a c i
6. Esboce o gráfico de uma função que seja continua exceto para a descontinuidade declarada.Descontinuidades em -1 e 4, porem continua à esquerda em -1 e a direita em 4