Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.5 - Ex. 6
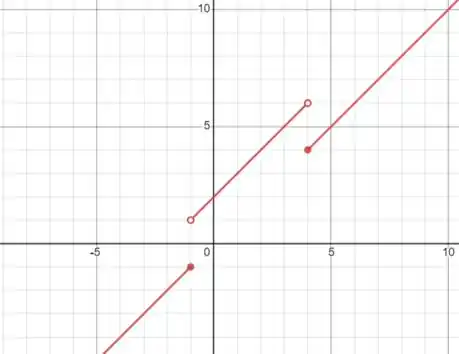
6. Esboce o gráfico de uma função que seja continua exceto para a descontinuidade declarada.
Descontinuidades em -1 e 4, porém continua à esquerda em -1 e a direita em 4
Passo 1
Opa, vamos fazer essa questão! O enunciado pede pra a gente esboçar um gráfico de uma função que seja continua à esquerda em e a direita em , com descontinuidade em e .
Aqui a gente pode usar QUALQUER função desde que a gente obedeça aos critérios que terminamos de ver! Lembrando que, para que a função seja contínua, a direita e a esquerda, respectivamente, devemos ter:
Mas para que ela seja descontinua em e , deveremos ter:
Caso o limite da função não exista nesse ponto, como em casos de limites laterais diferentes, também teremos uma descontinuidade.
É analisando essas condições que iremos encontrar nossa função. Veja que, a melhor estratégia aqui é utilizarmos de funções que são determinadas por mais de uma equação, encontrar apenas uma função que satisfaça todos os requerimentos pode ser MUITO difícil.
Passo 2
Vamos dividir em duas partes para ficar mais fácil e depois juntamos tudo! Para o ponto , temos:
Com isso, garantimos que ela vai ser continua a esquerda de , pois nesse ponto a função assume o valor e descontinua a direita, pois após esse ponto ela assume valor 1. De fato, teremos:
E
Passo 3
Para o ponto o raciocínio que iremos utilizar ser bem parecido, mas dessa vez nossa continuidade será à direita, então nossa função terá as seguintes equações em sua composição:
Podemos verificar que:
Veja que nossas funções são descontinuas nos pontos e pois seus limites laterais nesses pontos são diferentes, sendo assim, o limite para essas funções nestes pontos não existe.
Passo 4
Plotando o gráfico temos com o auxílio do GeoGebra, temos:
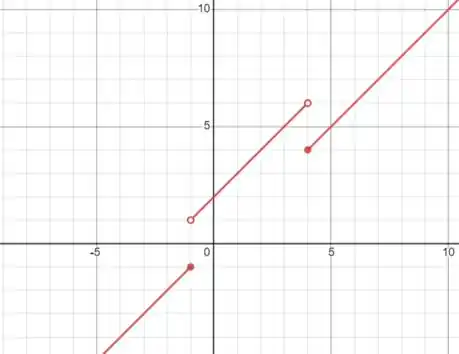
Basicamente temos aqui a representação da nossa função. Os pontos fechados indicam o valor da função no ponto dado, já os pontos abertos indicam o salto da função, a indefinição da função naquele ponto.
Resposta
