Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.3 - Ex. 68
Esboce o gráfico de uma função derivável que tenha:
- um mínimo local em (1, 1) e um máximo local em (3, 3);
- um máximo local em ( 1,1) e um mínimo local em (3, 3);
- máximos locais em (1, 1) e (3, 3);
- mínimos locais em (1, 1) e (3, 3).
Passo 1
- um mínimo local em (1, 1) e um máximo local em (3, 3);
- um máximo local em ( 1,1) e um mínimo local em (3, 3);
- máximos locais em (1, 1) e (3, 3);
- mínimos locais em (1, 1) e (3, 3).
Basta fazermos um gráfico qualquer tal que tenha um mínimo em (1,1) e um máximo em (3,3):
Passo 2
Agora basta escolhermos um gráfico com máximo em (1,1) e mínimo em (3,3):
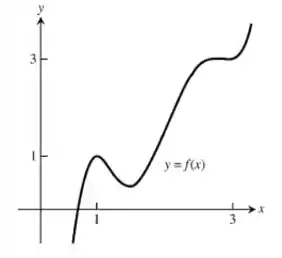
Passo 3
Agora vamos esboçar um gráfico com máximos em (1,1) e (3,3):
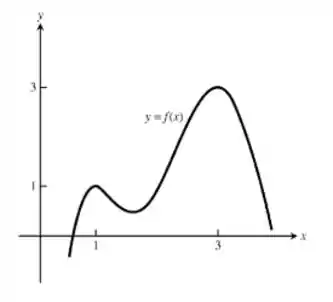
Passo 4
E, por fim, queremos um gráfico com pontos mínimos em (1,1) e (3,3)
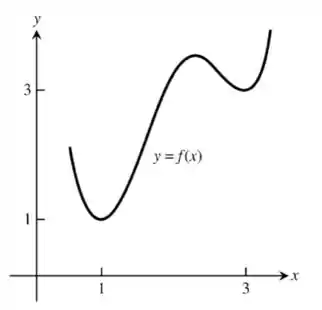
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o roteiro desta seção para esboçar a curva. y = e - x s e nx ,0xπ 2
O gráfico da função velocidade de um carro está mostrado na figura. Esboce o gráfico da função posição.
Trace um gráfico de f e use-o para fazer um esboço da primitiva que passe pela origem. f x = s e nx 1 + x 2 , - 2 π ≤ x ≤ 2 π
Trace um gráfico de f e use-o para fazer um esboço da primitiva que passe pela origem. f x = x 4 - 2 x 2 + 2 - 1 , - 1,5 ≤ x ≤ 1,5
( a ) Use uma ferramenta gráfica para fazer o gráfico de f x = 2 x - 3 x . b Começando com o gráfico da parte a , esboce um gráfico da primitiva F que satisfaça F 0 = 1 . ( c ) Use as regras dessa seç