Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 105
Esboce o gráfico da função duas vezes derivável com as seguintes propriedades. Quando possível, indique as coordenadas.
Passo 1
Sabemos que:
- se a função é crescente em x.
- se a função é decrescente em x.
- se x é um ponto crítico no gráfico (máximo ou mínimo absolutos)
- se a concavidade do gráfico é para cima em x.
- se a concavidade do gráfico é para baixo em x.
- se x é um ponto de inflexão (onde muda a concavidade)
A partir dessas informações, podemos esboçar a curva:
Passo 2
Primeiramente, marque os pontos dados:
Veja que quando a função é crescente, com a concavidade para baixo.
Temos um ponto mínimo em , pois a derivada primeira é zero, e a segunda é positiva.
Para valores de x entre 2 e 4, a função é crescente, com a concavidade para cima.
Temos um ponto de inflexão em , no ramo crescente.
No intervalo de , a função é crescente e tem a concavidade para baixo.
Temos um ponto de máximo em , pois a derivada primeira é nula e a segunda é negativa.
E por fim, para valores de , a função é decrescente e possui a concavidade para baixo.
Passo 3
Juntando essas informações, podemos esboçar o gráfico:
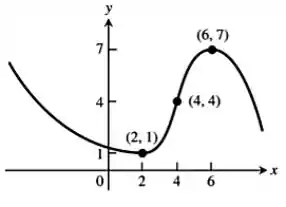
Resposta
Ei, a resposta está no passo a passo :)