Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 97
Esboce o gráfico da função racional:
Passo 1
Primeiramente, vemos que o domínio da função é (não pode zerar o denominador)
Podemos resolver isso derivando direto, ou simplificando primeiro. Vamos simplificar. Se dividirmos por (divisão de polinômio hein...) encontramos quociente e resto . Então, podemos reescrever nossa função como:
Vamos continuar...
Passo 2
Agora a gente encontra a derivada primeira e segunda...
Vamos encontrar os pontos críticos agora, que são onde a derivada é zero.
Pelo teste da derivada segunda: e
Então, temos um ponto máximo em e um ponto mínimo .
Passo 3
Vamos agora ver os intervalos de crescimento da função.
Sabemos que a função resulta em zero quando e e não está definida em .
Vejamos então...
Então, a função é crescente em e em e decrescente em (e .
Vejamos a concavidade...
Nossa derivada segunda deu , então vamos analisar o sinal nos intervalos anteriores:
Vemos então que será positiva se
Então, a concavidade é para baixo em e para cima em
A função muda a concavidade em , porém não temos um ponto no local já que ele não pertence ao domínio.
Vamos ter uma assíntota vertical em
Passo 4
Podemos encontrar ainda os pontos onde a função corta os eixos coordenados:
- Corta o eixo y em:
A função corta o eixo x em , como vemos na fatoração do polinômio.
Passo 5
Juntando as informações, temos o gráfico:
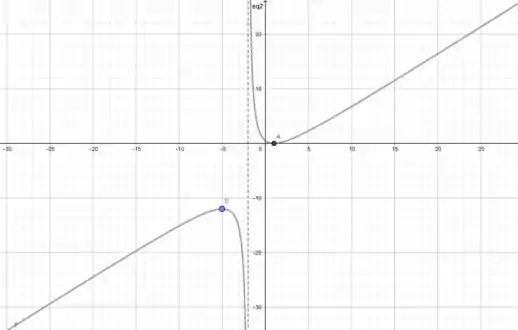
Resposta
Ei, a resposta está no passo a passo :)