Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.2 - Ex. 12
Esboce o gráfico da função e use-o para determinar os valores de para os quais existe:
Passo 1
Eaee, belezinha??? Bom... o enunciado nos deu a seguinte função:
Primeiramente queremos esboçar o gráfico dessa função.
Para isso, a gente observa que a função possui expressões para cada intervalo.
Assim, vamos plotar cada expressão como se fosse uma função (dentro no seu intervalo) e depois colocaremos tudo em uma só plotagem!
Com isso, poderemos determinar os valores de para os quais existe.
Agora bora lá!! 😉
Passo 2
Para a primeira expressão , sabemos que trata-se de uma equaç��o linear que representa uma linha descendente no plano cartesiano, onde o valor de é igual a menos o valor de .
Aplicando no intervalo , temos:
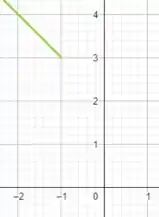
Para a expressão temos uma equação linear que representa uma linha diagonal ascendente no plano cartesiano, onde o valor de é igual ao valor de .
Aplicando o intervalo , temos:
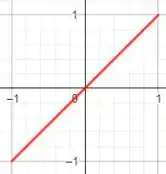
Por fim, para vemos que trata-se de uma parábola voltara para cima. E, aplicando o intervalo , temos:
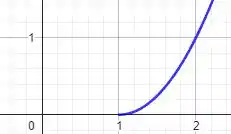
Passo 3
Juntando as plotagens, temos:
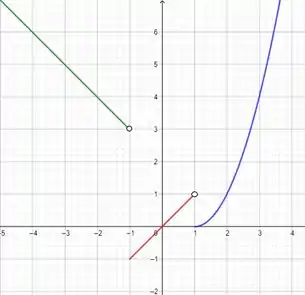
Passo 4
Pelo gráfico, o limite da função à esquerda de tende a , enquanto pela direita ele tende a , veja:
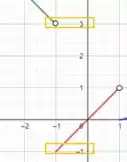
Como os dois limites são diferentes então não existe limite quando .
Agora, o limite da função à esquerda de tende a , enquanto pela direita ele tende a , veja:
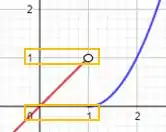
Como os dois limites são diferentes então não existe limite quando .
Para quaisquer outros valores, o limite dessa função existe.
Isso porque os limites laterais vão coincidir. Beleza?
Sendo assim, equivale a todos os números reais diferentes de , ou seja:
Prontinho!