Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.2 - Ex. 5
Para a função cujo gráfico é dado, diga o valor de cada quantidade indicada, se ela existir. Se não existir, diga o por quê.
Passo 1
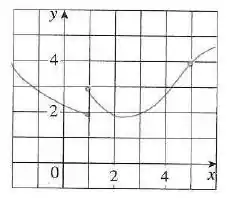
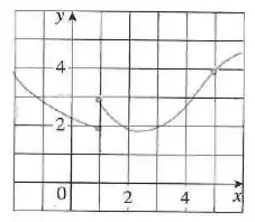
Opa, bora lá! O enunciado nos dá o gráfico:
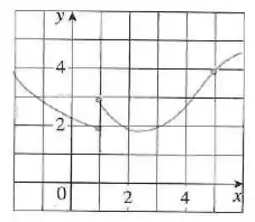
A partir dele a gente tem que dizer o valor de vários limites e se ele não existir, temos que dizer o motivo!
Para isso a gente tem que ter em mente que para o limite existir em um ponto a função tem que ser contínua nesse ponto!
Uma função contínua é aquela que a gente pode desenhar sem tirar o lápis do papel! Mas além disso aqui a gente vai pensar nos limites laterais, quando eles forem iguais pra um ponto o limite existe nesse ponto!
Podemos escrever assim:
Ou seja, se a gente se aproximar pela direita e pela esquerda, de um mesmo ponto, temos que chegar no mesmo valor! Agora bora lá!
Passo 2
Vamos trazer o gráfico pra pertinho da gente:
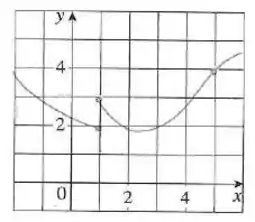
Vamos começar com:
Aqui é muito simples, olhamos pro gráfico e procuramos o saindo do eixo negativo e indo pro positivo. Aí achamos:
A bolinha ali é preenchida, então a função esta definida nesse ponto!
Passo 3
Agora vamos olhar para:
Nos aproximamos de pela direita:
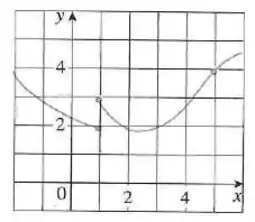
Então temos que:
Repara que não é e sim . Em temos a bolinha aberta indicando que a função não esta definida pra esse ponto!
Passo 4
Agora chegou a vez do limite de verdade:
Vimos nos passos anteriores que:
Como os limites laterais não existe, então não existe nesse ponto!
Passo 5
Agora vamos procurar no gráfico:
Podemos ver que, pela esquerda:
E pela direita:
Em a bolinha esta aberta, o que significa que a função não esta definida nesse ponto! Porém quando tende a tanto pela esquerda quanto pela direita nos aproximamos de .
Passo 6
Pra acabar devemos dizer o valor de !
Como terminamos de falar ali em cima, no lugar de temos uma bolinha aberta, portanto a função não esta definida!
Resposta
- não existe, pois os limites das letras (a) e (b) não são iguais
- não está definido, logo, não existe