Esboce o gráfico de
onde
Passo 1
Essa não tem muito segredo, vamos aplicar o limite e calcular a integral imprópria
Por definição
Então
Passo 2
Temos então que a função é apenas a deslocada, esboçando no plano:
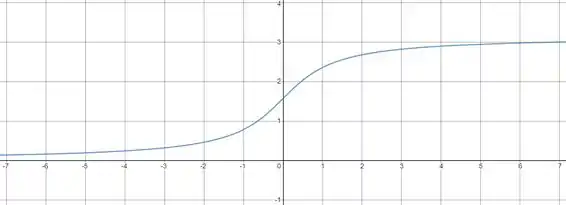
Resposta
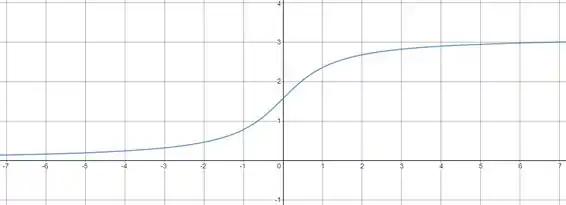
Esboce o gráfico de
onde
Essa não tem muito segredo, vamos aplicar o limite e calcular a integral imprópria
Por definição
Então
Temos então que a função é apenas a deslocada, esboçando no plano:

