Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 16

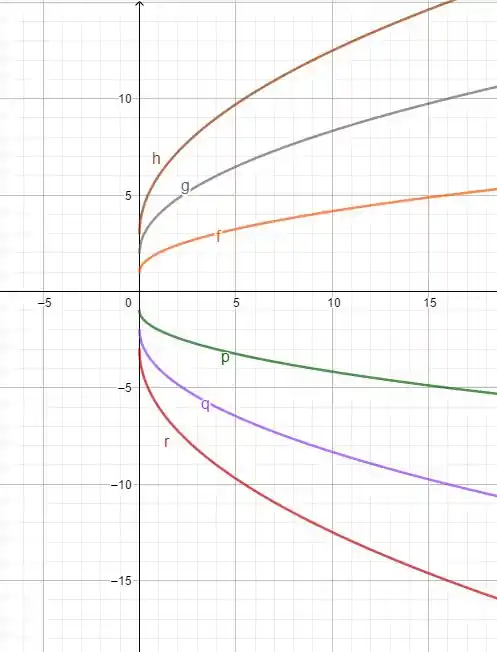
(a) Esboce o gráfico de y = a x com a = ± 1 , ± 2 , ± 3 em um único sistema de coordenadas.

(b) Esboce o gráfico de y = x + b com b = ± 1 , ± 2 , ± 3 em um único sistema de coordenadas.

(c) Esboce alguns membros típicos da família de curvas y = a x + b .

Passo 1

(a) Para esboçar y = a x , vamos pensar no gráfico de y = x , com algumas modificações: para valores positivos de a , teremos um alongamento do gráfico no eixo y e, para valores negativos, teremos uma reflexão pelo eixo x e um alongamento em y .

f ( x ) = x ;

g ( x ) = 2 x ;

h ( x ) = 3 x ;

p ( x ) = - x ;

q ( x ) = - 2 x ;

r ( x ) = - 3 x :

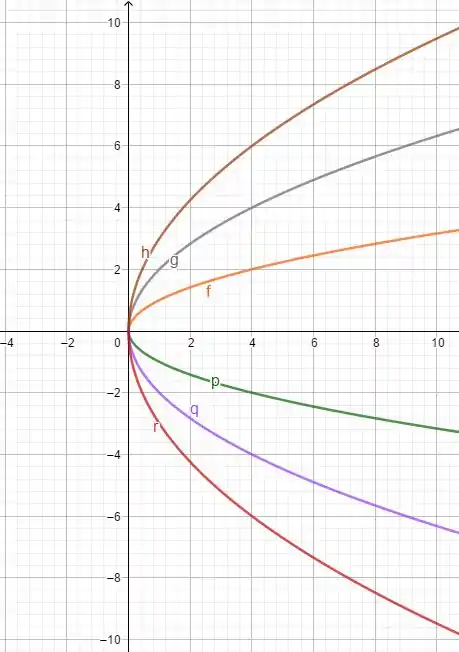
Passo 2

(b) Para esboçar y = x + b , vamos pensar no gráfico de y = x , com algumas modificações: para valores positivos de a , teremos um deslocamento do gráfico em b unidades para cima e, para valores negativos, teremos um deslocamento do gráfico em b unidades para baixo.

f ( x ) = x + 1 ;

g ( x ) = x + 2 ;

h ( x ) = x + 3 ;

p ( x ) = x - 1 ;

q ( x ) = x - 2 ;

r ( x ) = x - 3 :

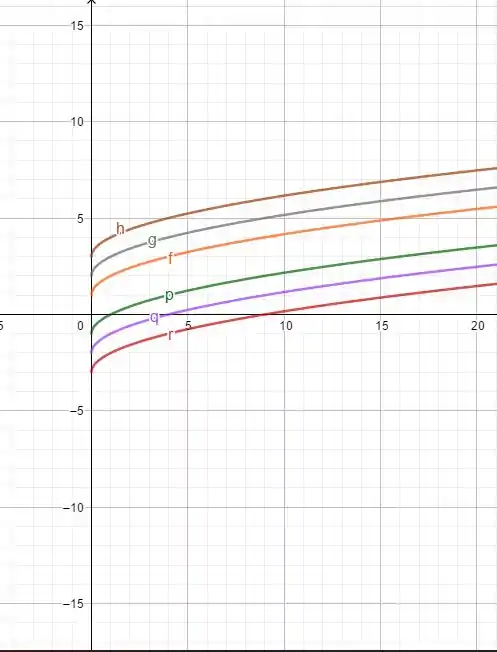
Passo 3

(c) Para esboçar y = a x + b , teremos a junção das duas letras anteriores, pois para diferentes valores de a teremos diferentes valores de alongamentos em y e os valores de b darão deslocamentos em y .

Alguns exemplos:

f ( x ) = x + 1 ;

g ( x ) = 2 x + 2 ;

h ( x ) = 3 x + 3 ;

p x = - x - 1 ;

q x = - 2 x - 2 ;

r x = - 3 x - 3 :

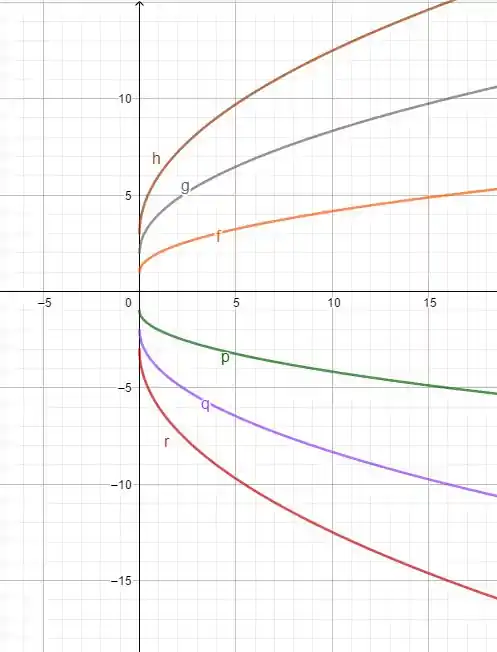
Resposta

(a)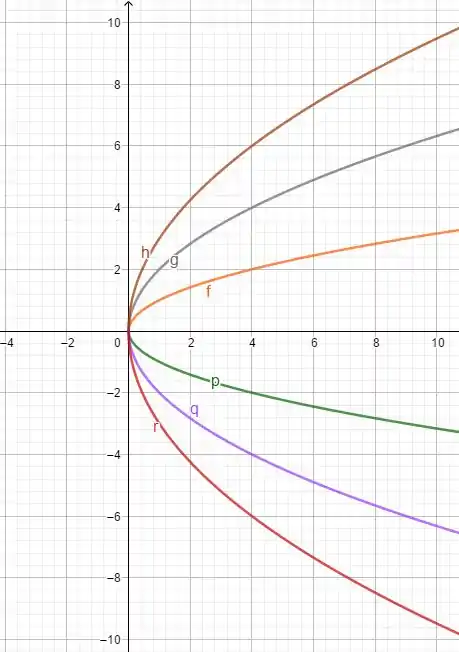

(b)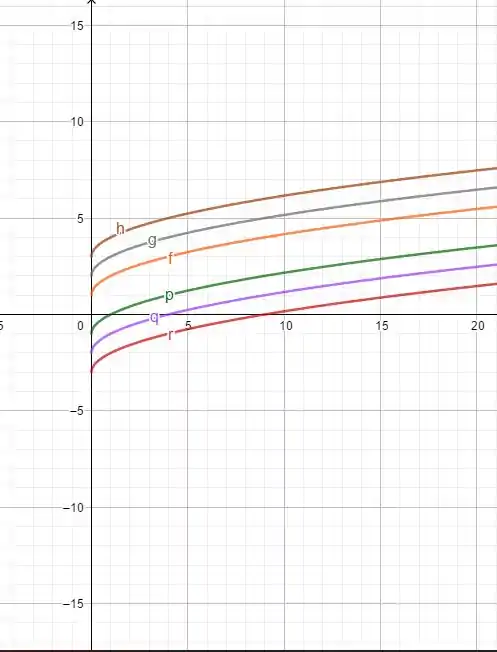

(c)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dada a função f x = x 2 + 1 , mostrar que, para a ≠ 0 , f 1 a = f a a 2
Dada a função f x = 1 x , mostrar que, para f 1 + h - f 1 = - h 1 + h . Calcular f a + h - f a .
Determine o domínio das funções. y = 4 - x 2
Se f x = x 2 + 2 x , achar f a + h - f ( a ) h , h ≠ 0 , e interprete o resultado geometricamente.
Exprimir o comprimento l de uma corda de um círculo de raio 4c m , como uma função de sua distância xc m ao centro do círculo.