Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 3
Esboce o gráfico de . Utilizando a ideia intuitiva de limite, calcule
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o gráfico da função e, usando a ideia intuitiva de limite, calcular:
Tá, mas que ideia intuitiva é essa? Isso quer dizer que nós vamos verificar de maneira menos formal, para que valor tende , para onde ela vai, quando se aproxima de . Repare que para , a função não está definida, por isso zeraria o nosso denominador. Então, vamos encontrar uma forma de simplificar a função para, em seguida, aplicar o limite.
Vamos lá!
Passo 2
Vamos começar esboçando o gráfico de :
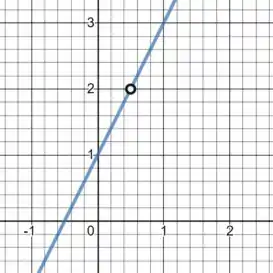
Podemos ver que não está definida para no gráfico, como tínhamos falado no passo .
Passo 3
Agora vamos tentar manipular a função dada por:
Como temos no numerador uma diferença de dois quadrados, podemos fatorar no produto da soma pela diferença dos termos, ou seja:
Simplificando por temos:
Desde que .
Passo 4
Então, para calcular o limite usando o resultado do passo anterior, sabemos que quando se aproxima de , então se aproxima de:
Logo:
Valeu, galera. Até a próxima! 😉