Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 1a
Esboce o gráfico da função dada e, utilizando a ideia intuitiva de função contínua, determine os pontos em que a função deverá ser contínua.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente esboçar o gráfico da função , usando a ideia intuitiva de função contínua. Mas que ideia é essa?
Dizemos que uma função é contínua se ela não apresenta saltos, ou seja, ela não tem interrupções, não é feita de pedacinhos. Se você for desenhar uma função contínua em um papel, usando um lápis, você vai passando o lápis na folha e não tira. Essa é a ideia intuitiva que o enunciado quer que a gente use.
Então, vamos lá!
Passo 2
Repare que a nossa função é uma função constante, então ela tem sempre o valor , independente do valor de .
Isso significa que estamos tratando de uma reta horizontal no plano cartesiano. Desenhando isso, vamos ter:
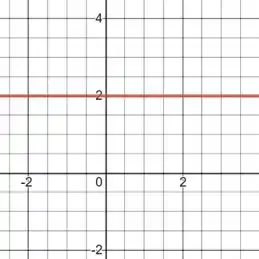
Podemos ver que não apresenta saltos, então podemos dizer que ela é contínua em toda a reta real.
Prontinho, galera. Até a próxima! 😉
Resposta
é contínua para todo .