Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.5 - Ex. 4
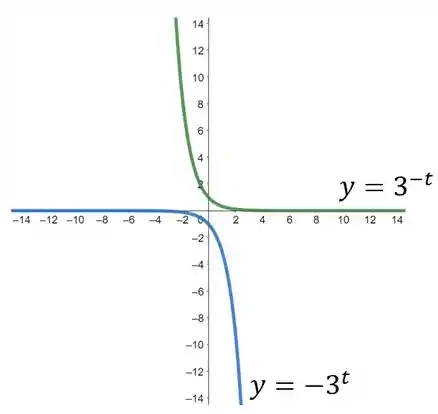
Esboce juntas as curvas dadas no sistema de coordenadas e identifique cada uma com sua equação:
Passo 1
Esta é uma questão que necessita que dois procedimentos sejam realizados: primeiro, o esboço das curvas. Em seguida, que estas curvas sejam identificadas. Fica claro que, ao plotar cada uma das funções, vocês saberão qual função corresponde a qual curva. Entretanto, aqui isto não será deixado claro inicialmente.
Por motivos didáticos, as curvas serão obtidas através de softwares. Após isto, elas serão relacionadas as suas funções a partir das suas características, como se é uma função de crescimento ou decaimento, por exemplo.
Passo 2
Vamos obter inicialmente o esboço das duas curvas.
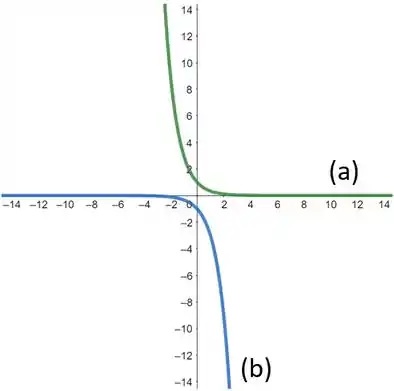
Passo 3
Agora, vamos identificar cada uma das curvas. A primeira função a ser estudada será . Esta é uma função de decaimento, devido a presença do sinal negativo multiplicando o expoente da exponencial. Além disto, como uma função exponencial é sempre positiva, ao ser multiplicada por outro número positivo , o valor de será sempre maior que zero. Desta forma, esta função é representada pela curva .
Consequentemente, a função é representada pela curva . Isto é confirmado ao observarmos que a curva é uma função de crescimento exponencial. A única diferença é que ela só assume números negativos, fato que decorre da multiplicação de toda a função exponencial por um número negativo . Se esta curva for rotacionada em torno do eixo , será observado facilmente uma função de crescimento.
Resposta
