Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.1 - Ex. 2
- Esboce, à mão, o gráfico da função , prestando particular atenção em como o gráfico cruza o eixo y. Que fato lhe permite fazer isso?
- Que tipos de funções são e ? Compare as fórmulas de derivação para e .
- Qual das funções da parte (b) cresce mais rapidamente quando é grande?
Passo 1
E aí! tudo certinho? 😉
Vamos lá já colocando a mão na massa porque a primeira coisa que o nosso problema pede é pra a gente esboçar um gráfico na mão!!
Veja só! 😉
Passo 2
E a gente tem que prestar atenção em quando o gráfico cruza o eixo . Um gráfico qualquer cruza o eixo quando , então:
Então a gente já sabe que é interessante que seja um dos pontos escolhidos!!
Agora a gente monta uma tabelinha com alguns valores:
Agora o gráfico:
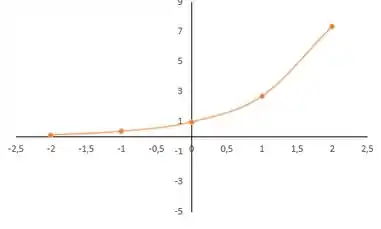
Tranquilo até aqui? 😬
Passo 3
Agora vamos para a letra (b)!
Aqui o problema traz duas funções:
e
E pergunta que tipo de funções são essas!
Temos duas funções crescentes! é uma função exponencial e é uma função potência.
A medida que aumenta, e também aumentam. Agora vamos ver suas derivadas:
Comparando as duas, vemos que, e é uma derivada de potência.
Bacana, não é? 😬
Passo 4
A letra (c) pergunta qual das funções cresce mais rapidamente! A derivada é a taxa de crescimento de uma função! Se:
Então cresce mais rapidamente que .
E aí! entendeu tudo? Responde Aí! 😉
Resposta
a)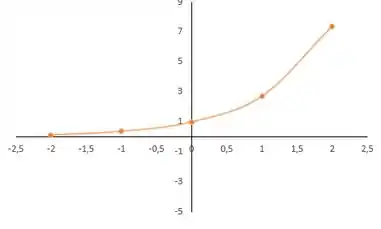 
b) e é uma derivada de potência.
c)