Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.3 - Ex. 2
Quais pares de coordenadas polares representam o mesmo ponto?
a.
b.
c.
d.
e.
f.
g.
h.
Passo 1
Fala, galera! Mais uma questão para a gente identificar pontos nas coordenadas polares. Alguns deles serão repetidos, então temos que descobrir isso. Como podemos expressar um mesmo ponto de formas diferentes apenas mudando o ângulo ou o sinal do raio . Por isso, vamos analisar todos os pontos com o mesmo valor de , em módulo.
Passo 2
Agora, vamos pegar todos com ou :
a.
b.
f.
h.
O ponto do item a tem raio e ângulo . Então, temos que ir até o ângulo e depois “voltar” duas unidades. Nesse caso, estamos no ponto . Já o ponto do item b também tem o mesmo ângulo, mas com raio negativo, o que significa que estamos no lado oposto do ponto a. Então, esse ponto não é igual ao primeiro. No item f, o ângulo é , então também temos um ponto igual ao primeiro. Finalmente, no item h, o ângulo mas o raio é negativo, o que significa que o ponto na verdade está no ângulo .
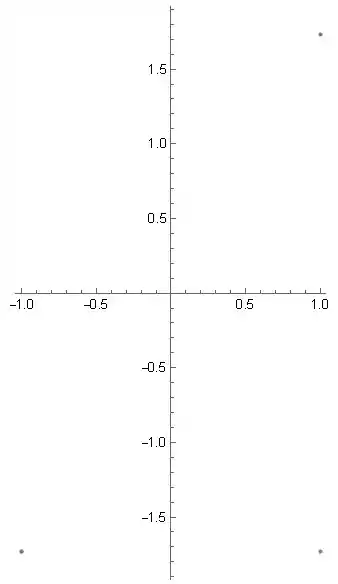
Passo 3
Agora, vamos analisar os itens
c.
d.
e.
g.
Vamos começar com o ponto . Se a gente girar esse ponto por um ângulo , caímos no ponto , que não é o mesmo que . O ponto é obtido a partir de apenas caminhando no sentido contrário unidades. Até agora, todos os pontos são diferentes. O ponto é obtido através de apenas caminhando no sentido oposto unidades ou a partir de , girando por um ângulo . Assim, todos os pontos estão em quadrantes diferentes.
Resposta