Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 8
Esboce a região cuja área é dada pela integral e calcule-a.
Passo 1
Fala, gente bonita! Tudo beleza??
Então, o enunciado pede pra gente esboçar a região cuja área é dada por essa integral aqui, olha só:
Precisamos calculá-la e achar a área, show?
Passo 2
Observa bem a integral. Por conta daquele , a gente sabe que estamos trabalhando com coordenadas polares. Relembrando alguns termos:
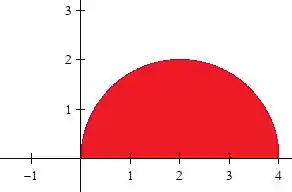
A região que estamos calculando corresponde à metade superior da circunferência de centro e raio .
Mas de onde veio isso?
De fato, note que
Se acrescentarmos dos dois lados...
E sabendo quem é cada um dos termos:
Organizando, teremos:
Com variando no intervalo , , o que restringe o domínio ao primeiro quadrante. Se pudesse variar até , teríamos um círculo completo com o quarto quadrante.
Passo 3
Para descobrir a área, calculamos primeiro a integral de dentro
Resolvendo...
Agora resolvendo a integral de fora, ou seja, em relação a :
Colocando o para fora da integral, descobriremos uma identidade trigonométrica na qual iremos fazer uma substituição:
Organizando um pouco mais, teremos
Onde podemos dividir essa integral em duas
Ou, de um outro modo, podemos dizer que a integral será igual a área de metade de um círculo de raio :
Belezinha? 😊