Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.8 - Ex. 3

3) Calcular ∬_R^() (d x d y)/(1 + x^2 + y^2) onde R é a região da Figura 7.34.

Passo 1

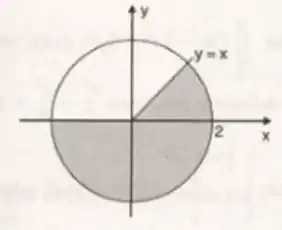
Ao analisar o gráfico, temos:

0 <= r <= 2

? <= theta <= ?

Pelas coordenadas polares, temos que:

x = r * cos theta

y = r * sen theta

Então para achar os valores de theta , temos que:

y = x

r * cos theta = r * s e n theta

c o s theta = s e n theta

Isso acontece quando o ângulo é de - pi , e o outro, pelo gráfico, podemos ver que o ângulo final é de (pi)/(4) . (CUIDADO para não confundir e inverter... senão vai calcular da parte branca)

- pi <= theta <= (pi)/(4)

Passo 2

Show, agora que temos as coordenadas polares e os limites de integração, vamos substituir e colocar na nossa nova integral! Não podemos esquecer do Jacobiano!

J a c o b i a n o = r

Dessa forma, temos:

x^2 + y^2 = r^2 * cos^2 theta + r^2 * sen^2 theta

cos^2 + sen^2 = 1

Logo,

= r^2 * cos^2 theta + r^2 * sen^2 theta = r^2

Dessa forma, temos:

∬_(0 - pi)^(2 (pi)/(4)) (r)/(1 + r^2) d theta d r

Passo 3

Primeiro vamos integrar com relação a theta ,

int_(- pi)^((pi)/(4)) (r)/(1 + r^2) d theta

Como estamos integrando em relação a theta , temos que esses r ’s todos ai são constantes, então ficamos com

((pi)/(4) - (- pi)) * (r)/(1 + r^2) (5 pi)/(4) ((r)/(1 + r^2))

Passo 4

Agora vamos integrar em relação a r ,

(5 pi)/(4) int_0^2 (r)/(1 + r^2) d r =

Vamos fazer uma substituição simples, chamar

1 + r^2 = u

d u = 2 r d r

(5 pi)/(4) * int (1)/(u) * (d u)/(2)

(5 pi)/(8) * ln |u|

Vamos voltar com a nossa substituição

(5 pi)/(8) * (ln |r^2 + 1||_0^2

(5 pi)/(8) * (ln |2^2 + 1| - ln |0^2 + 1|)

(5 pi)/(8) * (ln |5| - ln |1|)

Isso dá pra gente

(5 pi)/(8) * (ln |5|)

Resposta

(5 pi)/(8) * (ln |5|)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .6-
Calcule a integral iterada, convertendo-a antes para coordenadas polares.30- ∫ - a a ∫ 0 a 2 - y 2 x 2 + y 2 3 2d xd y
33- Uma piscina circular tem 40p é s é de diâmetro. Sua profundidade é constante na direção leste-oeste e aumenta linearmente de 2p é s é no término sul para 7p é s é no término norte. Determine o vol
Um aspersor distribuí água em um círculo de raio de 100 pés. Ele fornece água até uma profundidade e - r pés por hora em uma distância de r pés do aspersor.Qual a quantidade total de água fornecida po
Uma região R é mostrada. Decida se você deve usar coordenadas polares ou retangulares, e escreva ∬ R f x , y d A como uma integral iterada, onde f é uma função qualquer contínua em R .