Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.5 - Ex. 15

Esboce a região cuja área com sinal é representada pela integral definida e calcule a integral usando uma fórmula apropriada de Geometria quando for necessário.

a )   ∫ 0 5 2   d x c )   ∫ - 1 2 | 2 x - 3 | d x

b )   ∫ 0 π cos ⁡ x   d x     d )   ∫ - 1 1 1 - x 2   d x

Passo 1

Vamos esboçar cada uma...

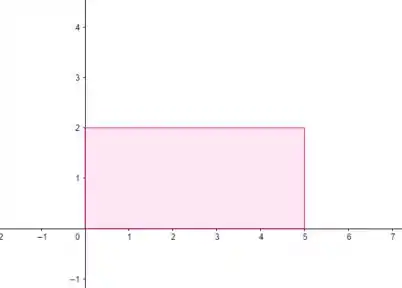
  1. Aqui a gente tem um retângulo, então é só a gente calcular a área dele de boas...

    ∫ 0 5 2   d x = 5 2 = 10

    Passo 2

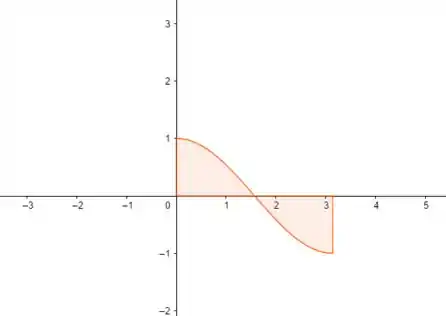
  2. Aqui a gente não tem uma figura geométrica direitinho pra calcular, mas se liga! A parte negativa é igualzinha a parte positiva, ou seja: a área líquida vai zerar!!

    ∫ 0 π cos ⁡ x   d x   = 0

    Passo 3

  3. Vamos pra terceira agora:

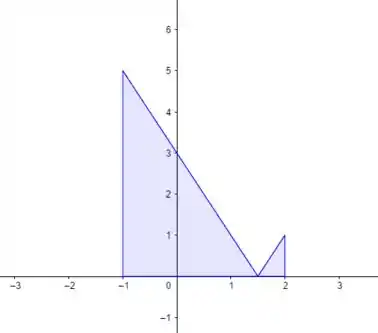
    4. Aqui a gente tem dois triângulos, os dois na parte positiva. Então a gente vai somar as duas áreas!

      ∫ - 1 2 | 2 x - 3 | d x = A 1 + A 2

    = 5 2 ⋅ 5 2 + 1 2 ⋅ 1 2

    = 25 4 + 1 4 = 26 4 = 13 2

    Passo 4

  4. Vamos ver essa última agora:

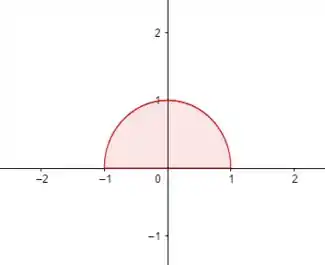
Aqui a gente tem um semicírculo de raio 1 , então é só a gente calcular a área dele😉

∫ - 1 1 1 - x 2   d x = π 1 2 2 = π 2

Prontinho!!

Resposta

  1. 1 0
  2. 0
  3. 13 2
  4. π 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o centroide da região.
Conforme indica a figura abaixo, as massas m 1 = 10 ,m 2 = 3 ,m 3 = 4 e m 3 = 4 e m estão posicionados numa certa viga sem peso com um fulcro colocado no ponto 4.Suponha que m = 14 . Sem calcular a so
Encontre o centroide da região.A região delimitada pelos gráficos de x = 1 y , x = 0 , y = 1 e y = 2 .
Encontre o centroide da região.A região delimitada pelos gráficos de y = x 2 e y = 1 .
Encontre o centroide da região.A região delimitada pelos gráficos de y = x e y = x 2 .