Esboce a região cuja área é:

e use seu esboço para mostrar que

Para a integral impropria , temos que a área é:

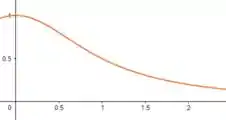
Lembrando que pela integral ela parte do ponto ao infinito e acaba passando pelo ponto !! Agora, para o segundo gráfico, temos:

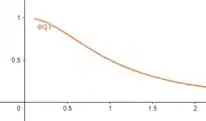
Este se assemelha simetricamente ao gráfico da integral imprópria e ainda tem pontos iguais ao intervalo do primeiro gráfico!

Prontinho!!