Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.13 - Ex. 18
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas.
Passo 1
Devemos começar as questões que pedem para calcularmos a área de uma região sempre pelo esboço dessa região. Se não esboçarmos ele, não conseguiremos compreender a integral que devemos calcular. Sendo assim, vejamos a região abaixo:
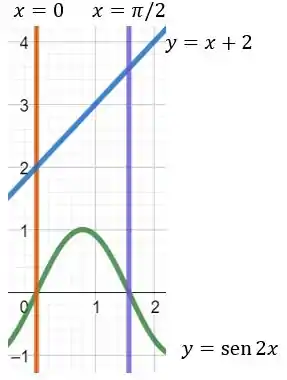
Como esta região é limitada acima e abaixo por uma curva, a área é dada pela seguinte integral:
Passo 2
Agora que conseguimos escrever a integral que nos dá a área, só nos resta calculá-la. Portanto, temos:
Portanto, a área da nossa região é:
Resposta
Exercícios de Livros Relacionados
Se x - for a coordenada x do centroide da região que fica sob o gráfico de uma função contínua f , onde a ≤ x ≤ b , mostre que ∫ a b c x + d f x d x = c x - + d ∫ a b f x d x
Um retângulo R com lados a e b foi dividido em duas partes R 1 e R 2 por um arco de parábola que tem seu vértice em um dos cantos de R e passa pelo canto oposto. Encontre os centroides de ambas as reg
Seja R a região que está entre as curvas y = x m e y = x n , 0 ≤ x ≤ 1 , ondem m e n são inteiros com 0 ≤ nm . a Esboce a região R . b Encontre as coordenadas do centroide de R . c Tente encontrar val
Calcule a integral, interpretando-a em termos das áreas. ∫ - 3 0 1 + 9 - x 2 d x
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 2 x d x