Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 26
Esboce a região delimitada pelas curvas fornecidas e encontre sua área.
Passo 1
Eaeee, belezinha?? Bom.. a questão nos pede para esboçar a região delimitada pelas seguintes curvas entre os pontos e :
E
Para isso, devemos calcular os pontos de interseção entre as duas curvas.
A questão também nos pede para calcular a área.
Em outras palavras, iremos utilizar a seguinte definição de área :
Onde essa área é representada na seguinte figura:
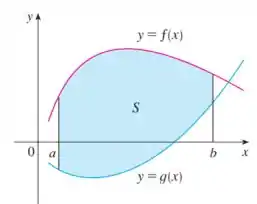
Dessa forma, devemos encontrar primeiro a interseção das curvas para prosseguirmos com o cálculo da área .
E aí?? Bora lá?? 😉
Passo 2
Para esboçarmos a região delimitada pelas curvas vamos esboçar ambas as curvas em um mesmo gráfico e, assim, vamos obter
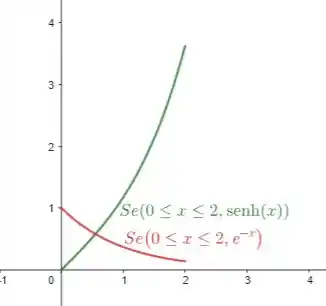
Para encontrar a área da região delimitada pelas curvas nesse caso, vamos ter que separar em duas partes haja vista que em um pedaço do gráfico temos uma função por cima e em uma outra parte outro gráfico está por cima.
Assim, devemos primeiramente encontrar o valor do ponto de intersecção entre as curvas igualando as suas equações obtendo
Passo 3
Assim, nossa integral vai ser dividida em 2 intervalos: de a e de a .
Então, nossa área vai ser