Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.5 - Ex. 18

Prove a distância do centróide de um triângulo é igual a um terço da altura daquele lado.

Passo 1

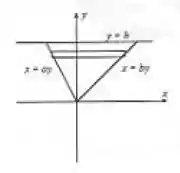
Vamos escolher o eixo x paralelo ao lado em questão, com a origem no vértice oposto a ele. O triÂngulo está desenhado na figura abaixo. O triângulo é formado pelas retas x = a y e x = b y ,   y ∈ [ 0 , h ] , e por y = h , onde h é o tamanho da altura.

Passo 2

Calculando a área temos:

A = lim ∆ → 0 ⁡ ∑ i = 1 n a m i - b m i ∆ i y   = ∫ 0 h a - b y d y A = 1 2 a - b y 2 0 h = 1 2 a - b h ²  

Passo 3

Vamos agora calcular o m y .

m y = lim ∆ → 0 ⁡ ∑ i = 1 n a m i - b m i m i ∆ i   y = ∫ 0 h a - b y ² d y m y = 1 3 a - b y 3 0 h = 1 3 a - b h ³

Passo 4

Vamos agora encontrar agora os pontos do centróide.

y - = m y A = 1 3 a - b h ³ 1 2 a - b h ² y - = 2 3 h

Resposta

A distância do centróide do lado dado é h - 2 3 h = 1 3 h .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Avalie a integral e interprete-a como a área de uma região. Esboce a região ∫ - 1 1 | 3 x - 2 x | d x
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a x ou y . Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a x ou y . Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da
Use um gráfico para encontrar as coordenadas x aproximadas dos pontos de interseção das curvas dadas. Então indique (aproximadamente) a área da região delimitada pelas curvas. y = 1,3 x ,y = 2 x
Esboce a região delimitada pelas curvas fornecidas e encontre sua área. y = 2 x 3 , y = x 2 / 8, 0 ≤ x ≤ 6