Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 16
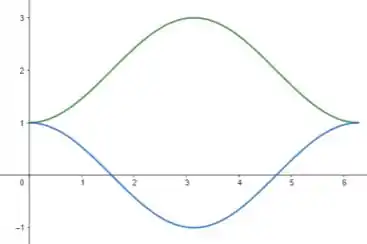
Esboce a região delimitada pelas curvas indicadas e encontre sua área.
Passo 1
Eaee, belezinha?? Bom... queremos esboçar a região delimitada pelas seguintes curvas:
E
No intervalo .
E, posteriormente, devemos calcular a área entre as duas curvas.
Para isso, temos que saber do seguinte teorema:
A área da região limitada pelas curvas e pelas retas e , onde e são contínuas e para todo em , é:
Agora vamos lá aplicar!! 😉
Passo 2
A gente sabe que a função cosseno é esboçada da seguinte forma:
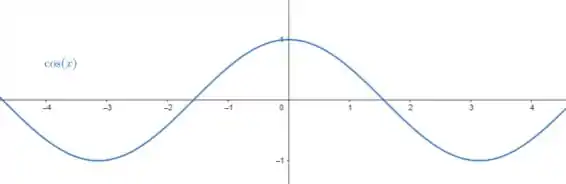
Dessa forma, a função é a mesma coisa da figura acima, com a exceção de que estamos “subindo” o gráfico em unidade e invertendo ele (pois tem um sinal negativo no cosseno), veja:
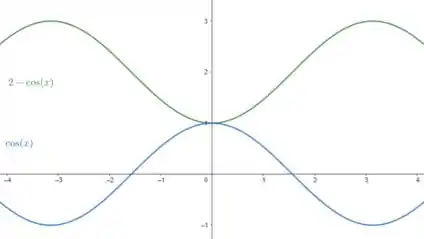
Assim, aplicando a região delimitada por , obtemos:
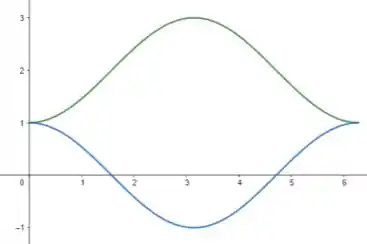
Passo 3
Nesse sentido, para calcularmos a área delimitada pelas duas curvas, aplicamos o conceito mostrado no Passo 1 e utilizamos o intervalo dado como limites de integração:
Resolvendo essas integrais:
Então,
Entendeu direitinho?? Responde aee 😉
Resposta
